Whenever Mythbusters meet bullets — no, not literally, though this week’s episode of Mythbusters does have Adam and Jamie trying to shoot cardboard cutouts of themselves — you know something wacky and interesting is about to ensue. The myth in question is that, with an unwisely aimed shot, it’s possible for a bullet to bounce off three steel beams and come back to hit the shooter.

Seems straightforward enough, right? If the beams, or walls as the case may be, are lined up at right angles to each other, why shouldn’t a bullet just bounce off all three and come right back to where it started?

As Adam and Jamie (re)discovered during the show, bullets don’t bounce, at least not when they’re moving as fast as, well, a speeding bullet. They shatter on contact with any hard enough surface, like steel, and the pieces spray out in what could be a completely different direction from what you’d naively predict.

From a physics perspective, this highlights the difference between elastic and inelastic collisions. Elastic collisions are based on the idea of a ball bouncing off a wall; it goes in at some speed and bounces right back at the same speed, at the same angle, like a laser bouncing off a mirror. The key characteristic is that the ball exits with the same amount of energy it came in with, and that’s what defines an elastic collision: no kinetic energy is lost (except in experiments with subatomic particles, where “elastic collision” means something slightly different, but that’s another story).

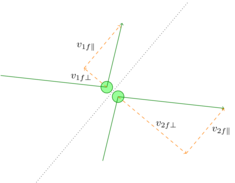
The nice thing about elastic collisions is that they’re easy to analyze. If we know the orientation of the surface along which two elastically colliding bodies are going to contact each other, the laws of conservation of momentum and energy,

are enough to determine the final velocities of both objects. You just decompose the momentum (or velocity) into components parallel to and perpendicular to the collision surface; the parallel components are unaffected, and you can solve the equations for the perpendicular components. They work out to

Unfortunately, most collisions in the real world (again, this doesn’t quite apply when you consider the microscopic view) are inelastic collisions, which do involve a loss of kinetic energy. The archetypal example of this is two lumps of clay, or perhaps bread dough, smacking into each other. Instead of bouncing away like rubber balls, they stick together and continue to move with one combined velocity, \(v_f\) (try it!), which is most certainly not what the solutions for \(v_{1f\perp}\) and \(v_{2f\perp}\) describe. So if the answer doesn’t correspond to reality, unless the math is wrong (and it’s not, I checked), one or more of the underlying assumptions must be wrong.

Experiments have shown that conservation of kinetic energy is that wrong assumption. What actually happens in an inelastic collision is that some of the kinetic energy gets transformed into some other form — heat, sound, maybe even light if the right materials are involved… but one of the most common destinations for extra energy is deformation. Real objects are not perfectly rigid; they can be squashed, squeezed, extruded, twisted, dented, bent or broken in various ways. All of that takes energy. The reason inelastic collisions are so hard to analyze is that there are so many different ways in which the energy can be used up, and exactly how much energy goes where depends on the detailed properties of the objects colliding. There’s practically no way to figure out what really goes on inside a collision at the level of detail needed to calculate it from scratch.

But never fear, physics has not failed us yet ;-) The coefficient of restitution \(C_R\) is a simple variable that describes, at the macroscopic level, how objects are affected by collisions: it’s defined as the ratio of final velocity difference to initial velocity difference, in the direction perpendicular to the collision plane.

For elastic collisions, \(C_R = 1\), which makes that definition equivalent to the conservation of momentum (the minus signs in the definition come from the fact that the two objects’ velocities are in opposite directions). By analogy, we can write the conservation of perpendicular momentum for an inelastic collisions, \(C_R < 1\), as

and the solutions for the final velocities become

The example of the two lumps of clay colliding is an extreme case, where \(C_R = 0\), although that extreme case is not too far off from the bullet-on-steel impacts the Mythbusters measured.

If this were a full-blown research project, I might try to make a rough calculation of the coefficient of restitution for bullet-on-steel impacts, using the more fundamental properties of the various metals involved. But that would take way more time than I have right now (too bad, because I’m really curious to know how accurate of a model I could come up with… oh well, maybe someday). To do something quickly, let’s just see what kind of a coefficient of restitution would be required for the \(\unit{360}{\degree}\) ricochet Adam and Jamie were looking for.

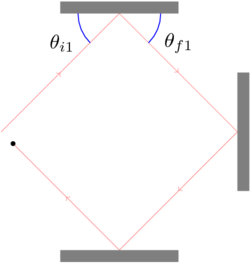
I’m going to make a couple of assumptions that are not exactly correct, but I hope they’re going to be close enough:

1. The steel plates (walls) don’t move
2. The only force on the bullet is perpendicular to the plate

Here’s why: assumption #1 means the velocity of the plate, let’s call it object 2, is negligible. So the coefficient of restitution simplifies to

Assumption #2 means that the component of the bullet’s velocity parallel to the plate stays the same during the collision, \(v_{f\parallel} = v_{i\parallel}\). Now I can use the fact that \(\tan\theta_{i} = v_{i\perp}/v_{i\parallel}\), and similarly for the outgoing angle, to write

The second assumption also means that the parallel component of the bullet’s momentum is conserved,

With a little creative algebra, I can combine this with the expression for \(C_R\) to give

The first thing to look at is the problem that Adam and Jamie kept coming up against: the collisions they were getting slowed their bullets and ball bearings down to the point where the shot would no longer be lethal once it got back to the shooter. The target velocity they were aiming for was about \(\unit{300}{\frac{\foot}{\second}}\). Given that these bullets emerge from the gun at about \(\unit{800}{\frac{\foot}{\second}}\), in order for a ricochet to be lethal, we need the product of the three factors

to be greater than \(\frac{3}{8}\). (By the way: a third assumption is in order here, that \(C_R\) depends only on the materials involved in a collision and not on the angle of impact or the velocity. This is not exactly true, but again, I hope it’s close enough for demonstration purposes.)

I’m going to look at a simple case: let’s assume that the walls are oriented at \(\unit{90}{\degree}\) angles, to form a rectangular area for the bullet to ricochet around in. That tells us a specific relationship between the final angle of each collision and the initial angle of the next, namely that they add up to \(\unit{90}{\degree}\), so the cosine of one is the sine of the other, and vice versa. This means that

Now here’s something interesting I discovered: if you take the first two factors modifying the ricochet velocity,

and plug in for \(\theta_{2i}\) in terms of \(\theta_{1i}\), you get

which is to say that under these particular conditions, regardless of the angle, a bouncing bullet’s velocity drops by a factor of \(C_R\) after two bounces! This makes the calculation considerably prettier, since the product of three square roots from above reduces to

Remember, this just has to be larger than \(\frac{3}{8}\) to make a successful kill. It’s easy enough to plot it for some reasonable values of \(C_R\) to see if it’s going to work:

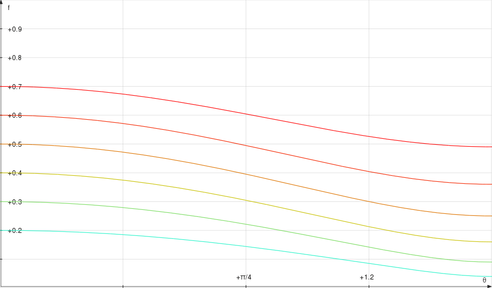
From the Mythbusters’ experiments with cinderblocks, I calculate \(C_R = \frac{\tan\theta_f}{\tan\theta_i} \approx 0.4\), the yellow line in the plot, which means they might just be able to keep the bullet going fast enough… or rather, might have been, if these calculations were at all accurate ;-) In reality, it didn’t quite work, and I’m not surprised because I’ve been making some pretty optimistic assumptions.

It’s certainly been evident that this problem has exploded in complexity — certainly I had no idea what I was getting in to when I started writing! And we’re still stuck on the rectangular box model, which only worked because of that fortunate substitution \(\cos\theta_{2i} = \sin\theta_{1f}\). What about arbitrary orientations, like the final cinderblock trial on the show? I don’t know if there’s any way to get an analytic solution, but this strikes me as an ideal opportunity to switch over to computational methods and demonstrate an evolutionary algorithm that selects the best candidates for reflected kill shots. But that’s a project for another day. I’ll have to leave off with this teaser graph that shows some different bullet trajectories in the rectangular box model. Color represents initial angle, opacity represents final velocity; and it’s easy to tell that nothing moving fast enough to be lethal quite makes it back to the point of origin…

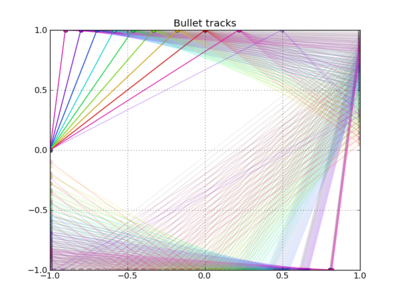
I guess one point of this is clear: if you’re going to shoot yourself, better point the gun at your head.