Balloons as air bags: is there any hope?

Posted by David Zaslavsky on October 15, 2012 8:02 PM — Edited October 15, 2012 8:20 PM

— Comments

It’s time to write about Mythbusters again! Last night on the show, the team tested a myth that balloons can take the place of an air bag in the front seat of your car, and if you have the right configuration of balloons, you’ll be protected from the damaging effects of a crash.

If you watched the show, you’ll know that this myth was thoroughly busted. The maximum acceleration a human body can take and still survive is $100g = \SI{980}{m/s^2}$, and no matter what configuration of balloons they tried, they were unable to reduce the acceleration to any less than about $120g$. This got me thinking about why that might be the case. Physically, keeping a body’s acceleration below a certain threshold is just a matter of spreading that acceleration out over a long enough distance. It’s easy to see that by looking at the relevant equation:

$$v^2 = v_0^2 + 2a\Delta x$$

For a car crash, you’d be given $v_0$, the initial speed, and $v = 0$, the final speed, and so if you want $a$ to be small, you have to make $\Delta x$ large. Specifically,

$$\abs{\Delta x} \ge \frac{v_0^2}{\abs{a}}$$

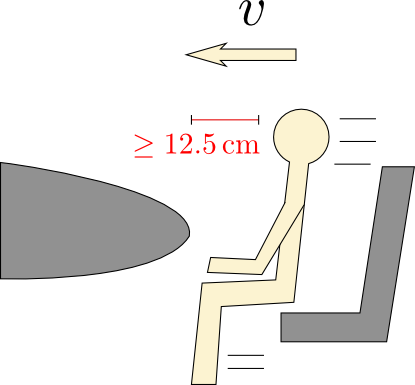person in car with 12.5 cm margin For an initial speed of $\SI{35}{mph}$ and $a = 100g$, that works out to about $\SI{12.5}{cm}$. Essentially, your body has to decelerate for at least $\SI{12.5}{cm}$ further after your car crashes, otherwise you die. This is how seatbelts and airbags work: they apply enough resistance to slow you down before you smack into the dashboard, but not so much to stop you within that critical distance. Smacking into the dashboard (or windshield), of course, pretty much stops you on the spot. That’s bad.

Now, $\SI{12.5}{cm}$ is not actually that far. A typical car will give you significantly more space than that in the passenger seat (where this myth takes place), probably about $\SI{50}{cm}$ to the windshield and $\SI{25}{cm}$ from your midsection to the dashboard. So with an appropriate mechanism to slow you down (again, hint: seatbelt, airbag), you’ll be okay in a $\SI{35}{mph}$ crash. Balloons, though, are probably not that mechanism. They’re designed to hold their shape, not to squish like an airbag, which is really more akin to a pillowcase.

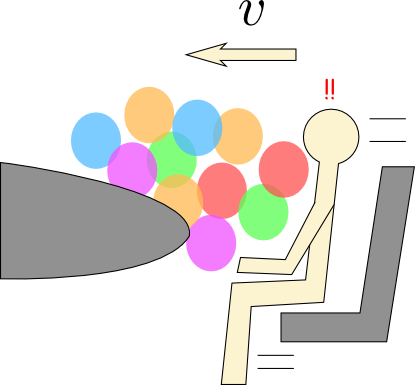person in car with balloons In fact, let me throw a bit of math at this. A balloon is roughly a pocket of ideal gas. When it gets compressed quickly, as it would in a car crash, it doesn’t have time to exchange heat with its surroundings and thus it will approximately follow the PV relation for an adiabatic process, $PV^\gamma = \text{const}$, where $\gamma\approx 1.6$ for helium. Now suppose the balloon is a box (if a cow can be a sphere, a balloon can be a box!) and that it’s getting compressed in one dimension. The pressure of the balloon as a function of its current thickness $l$ is

$$P = P_0 \biggl(\frac{V_0}{V}\biggr)^\gamma = P_0 \biggl(\frac{A l_0}{A l}\biggr)^\gamma = P_0\biggl(\frac{l}{l_0}\biggr)^{-\gamma}$$

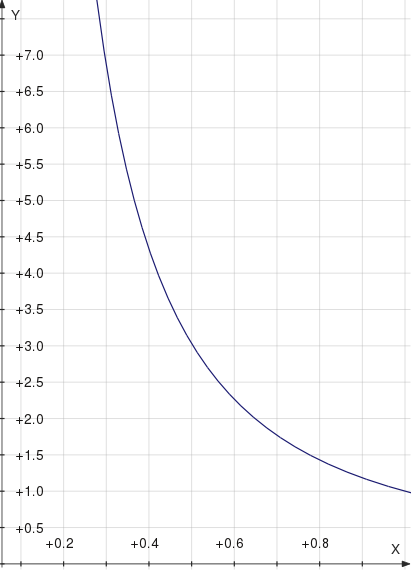
This means the force it exerts, $F = PA$, scales as $l^{-1.6}$. That’s pretty fast. As you can see from the graph, every time the balloon is compressed by a third, the force doubles. Would a balloon even be able to stop a person before its restoring force gets high enough to provide that $100g$ acceleration?

graph of pressure vs. distance

Well, the work needed to compress the balloon to a given thickness $l$ is

$$W = -\int_{l_0}^{l} F\udc l = -\int_{l_0}^{l} P_0A\biggl(\frac{l}{l_0}\biggr)^{-\gamma}\udc l = -\frac{P_0Al_0}{1 - \gamma} \biggl[\biggl(\frac{l}{l_0}\biggr)^{1-\gamma} - 1\biggr]$$

(the negative sign comes because I’m calculating work done on the balloon, but $F$ is force exerted by the balloon). Now suppose you have a person’s torso flying at this balloon at $v_0 = \SI{35}{mph}$. It has a kinetic energy $\frac{1}{2}mv_0^2$, and can accordingly do that much work. Setting the expressions equal, we get

$$\begin{align}-\frac{P_0Al_0}{1 - \gamma} \biggl[\biggl(\frac{l}{l_0}\biggr)^{1-\gamma} - 1\biggr] &= \frac{1}{2}mv_0^2 \\ \biggl(\frac{l}{l_0}\biggr)^{1-\gamma} - 1 &= \frac{\gamma - 1}{2P_0Al_0}mv_0^2 \\ l &= l_0\biggl(\frac{\gamma - 1}{2P_0Al_0}mv_0^2 + 1\biggr)^{\frac{1}{1-\gamma}}\end{align}$$

The acceleration of the torso at this balloon thickness $l$ is in turn given by

$$a = \frac{F}{m} = \frac{P_0A}{m}\biggl(\frac{l}{l_0}\biggr)^{-\gamma} = \frac{P_0A}{m}\biggl(\frac{\gamma - 1}{2P_0Al_0}mv_0^2 + 1\biggr)^{\frac{\gamma}{\gamma - 1}}$$

Umm… isn’t that a fun-looking formula?

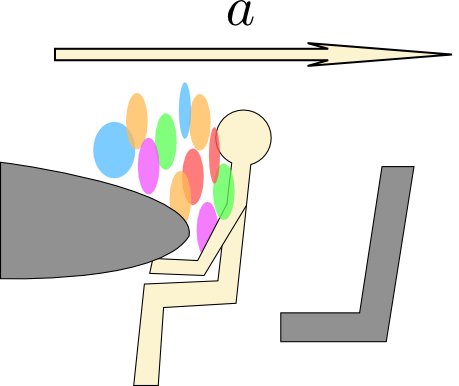person in car with squished balloons, experiencing acceleration Fortunately, it’s time to plug in numbers. I’ll guess $P_0 = \SI{820}{mmHg}$ (see this video), $m = \SI{20}{kg}$, $A = \SI{300}{cm^2}$ for a face, and treating the whole stack of balloons as a single large balloon, $l_0 = \SI{30}{cm}$. With these numbers, I get a final acceleration of $a = \SI{1870}{m/s^2}$, or $191g$ — well over the critical value for death! This happens as the stack of balloons is squished to a fifth of its original size, and is subjected to more than five times atmospheric pressure.

Only if you bump the thickness of the balloon stack $l_0$ up to about $\SI{50}{cm}$ do you get under the survivable limit.

Of course, in reality the balloons would pop long before this happens. They can’t take much of an increase over atmospheric pressure. So what happens when a balloon pops? It breaks the rubber which was providing resistance to the person’s head, and that means no more cushioning from that balloon. So breaking balloons actually means you can fly further forward in the car without being slowed, and that in turn gets you closer to the windshield, dashboard, and death by “instant” acceleration.