If you care at all about (American) football, or are trying to pretend you do, you probably saw the power go out during the Superbowl this past Sunday. Half the stadium lights, the scoreboard, and the announcers’ booth, completely out of commission. Hey, did you know there are actually people talking during the game most of the time?

Anyway, one of my friends made an offhand comment about people holding their phones up like candles, but it got me thinking, XKCD-style: what kind of light could you get on a football field from cell phones? Enough to play? Or would you have to give everyone xenon lamps? To find out, we have to delve into the, um, murky world of photometry, the science of measuring the perception of light.

Let’s start with something simple. Anyone who’s familiar with a bit of physics knows about power: the amount of energy per unit time. When you characterize a light bulb as a hundred-watt bulb, for instance, that’s a measure of the power it puts out when attached to the circuitry of a standard lamp. There’s a whole hierarchy of other measurements you can make that are all derived from power: the power per unit area, power per unit solid angle, power per unit wavelength, and so on.

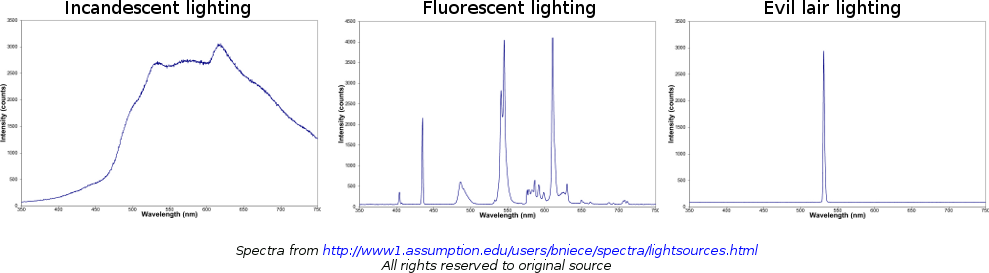
But power doesn’t tell the whole story. In order to light a football game, what you need is not a particular amount of power, but an amount of perceived brightness, which is not the same thing. They’re different because the eye doesn’t respond to all wavelengths equally. We normally have the strongest response in the green part of the spectrum, which means that a given power of green light will appear brighter than the same power of red light, or blue light. For example, a green milliwatt laser will look brighter than a red milliwatt laser (in the instant before they destroy your retina), even though they both have the same power. As a more extreme example, incandescent light bulbs emit a lot of their energy in infrared radiation, which the eye doesn’t respond to at all. Even though a bulb might use a hundred watts of power, it produces a level of brightness that only takes about 5 of those watts to create. This is why fluorescent bulbs are so efficient: they match the brightness of an incandescent bulb by giving off similar amounts of power in the visible spectrum, without all the wasted infrared radiation. If you wanted even more efficient lighting, you could use green fluorescent bulbs. (A key step in turning your home into an evil lair.)

Photometry uses its own hierarchy of measurements:

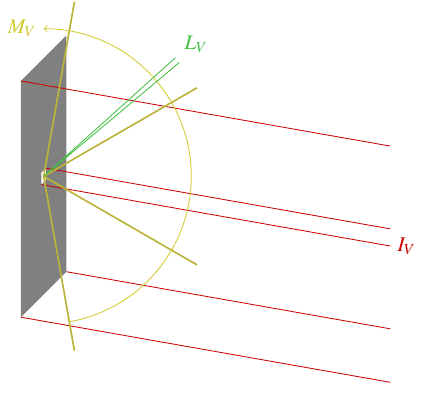
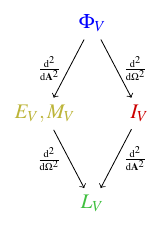
• The photometric equivalent of power is the luminous flux, \(\Phi_V\), which is the total effect of all the light emitted from all parts of an object in all directions. It’s measured in lumens. You can characterize the lighting ability of a light bulb, for instance, by its luminous flux. (Look on the package, you’ll find a number of lumens printed there.)
• You can break down the luminous flux emitted (or received) by an object by its direction. The luminous flux per unit solid angle is called the luminous intensity, \(I_V\), measured in candelas (lumens per steradian). Luminous intensity reflects the object’s actual perceived brightness as you’re looking at it from a particular direction.
• You can also break down luminous flux by surface area. The luminous flux per unit surface area is called illuminance, \(E_V\), if it’s the flux per unit area of the object being illuminated, or luminous emittance, \(M_V\), if it’s the flux per unit area of the emitter. In either case, the unit is the lux, a lumen per square meter. Luminous emittance characterizes the ability of, say, an array of bulbs to emit light; obviously the larger you make the array, the more light it will emit, but the luminous emittance normalizes that by dividing by the area. And illuminance is what determines your eye’s ability to see something: it has to exceed the amount of luminous flux needed to stimulate a cell on your retina divided by the area occupied by that cell.
• Of course, you can break luminous flux down both ways as well: the luminous flux per unit solid angle per unit area is the luminance, \(L_V\). This is measured in candelas per square meter, also known as nits. (There’s no shortage of funny non-SI unit names in this business.) Luminance represents the perceived brightness of a bright object per unit area. Because luminance normalizes for both surface area and solid angle, it’s the quantity of choice to measure the perceived brightness of a computer display or cell phone screen from a particular direction.

OK, so what are some typical values for the luminance of a phone display? The very popular iPhone 5 gets 562 cd/m^2. But it’s a hypothetical situation, so let’s go all out: the brightest actual cell phone screen I could find evidence for is the Nokia 701, at 1000 cd/m^2.

To compare the stats for a phone to the required lighting on the field, we’ll need to calculate the illuminance a single cell phone produces on the field. Illuminance is luminance times solid angle, so we integrate the luminance of the cell phone’s screen over its angular size as seen from the field:

\(L_V\) can be considered constant over the phone’s screen, and if the screen is pointed right at the field from above, \(\cos\theta = 1\), so this is just a multiplication. And solid angle is equal to area divided by the distance between the phone and the field squared, so

Now we get to add this up for one phone for each person at the Superbowl. All 71024 of them. That’s a lot of phones.

As you might guess, getting an exact answer would be pretty complicated, but maybe we can get away with a “physicist’s shortcut:” let \(r_\text{min}\) be the distance of the closest seat to the center of the field (front row, 50-yard line). Based on the standard dimensions of an NFL field \(r_\text{min}\) should be a little over \(\SI{106}{ft.}\), but I’ll underestimate and use that actual value. Suppose every one of those 71024 phones was at that distance. With \(L_V = \SI[per-mode=fraction]{1000}{\candela\per\square\meter}\) per phone, \(A_\text{phone} = \SI{34}{cm^2}\) (source), the total illuminance is

I couldn’t find any data on lighting levels recommended by the NFL, but for the NCAA football championship, the recommended lighting level is 125 foot-candles [PDF], which is equal to \(\SI{1345}{lx}\), to the camera at the 50-yard line. Even if all 71024 cell phones were pointed directly into the camera, straight on, they wouldn’t produce enough light to meet that threshold. Not even close. So replacing the normal Superbowl lights with a sea of cell phones is not going to work.

In the spirit of XKCD and Mythbusters, what would it take? Well, we’ve already calculated \(E_{V,\text{max}}\), and it’s proportional to both the luminance and the phone area. So as a minimum baseline, we need a phone that’s either six times bigger or six times brighter. Maybe a tablet? The Panasonic Toughpad FZ-G1 has a 10.1-inch screen, with an area of \(A_\text{tablet} = \SI{315}{cm^2}\), and a luminance of \(L_V = \SI[per-mode=fraction]{800}{\candela\per\square\meter}\).

Now we’re talking. So stadium designers, listen up: just spend the $205 million to slip a Toughpad under every seat in case of power outage, and you’ll be fine.

Except not really. \(E_{V,\text{max}}\), after all, is not the actual illuminance that will be delivered to a TV camera, first, we’re still using an extremal model where all the phones (or tablets) are right at the edge of the field. Also, the numbers I’ve been calculating are for a surface receiving light directly from the phones — they only apply if every phone is pointed directly into the camera. In reality, the cameras pick up the reflection off the field, the football, the players, or whatever else they’re pointed at, so we’ll need to include a factor to account for that.

First, I’m going to come up with a more accurate estimate of the light delivered by phone screens which are actually placed in the stadium seats. The obvious way to do this would be to add up the contributions from the seats by row, but that’s not so easy because the seats in a row aren’t all at the same distance from the field, plus there are partial rows, plus there aren’t even the same number of seats in each row. If you had access to an exact blueprint of the seating area of the Super Dome, you could crunch the numbers, but I don’t, and besides, that would be excruciatingly complicated.

Instead, I’ll construct a toy model of the stadium’s layout, and assume the seats are continuously distributed throughout the seating area of this model. The model is going to look like this:

Angle view	Top view

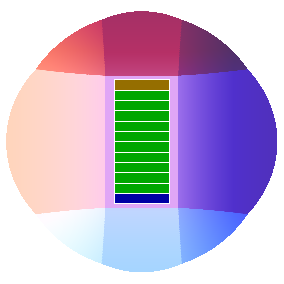It’s basically a circular seating region with diameter \(\SI{680}{ft.}\), with a rectangle of \(\SI{384}{ft.}\times\SI{212}{ft.}\) cut out of the middle for the field. It doesn’t take into account that the stadium has three tiers of seating that partially overlap, or that the seating region is actually slightly elliptical, but I think this should be good enough as a first approximation.

The first thing I’m going to need is the average area per seat — or rather, the average seating area per person.

Armed with that number, I can calculate the total illuminance at the center of the field like this:

I’m integrating the illuminance per phone, including the cosine factor which accounts for the phone’s light coming in at an angle, over the seating area, and then dividing by the area per seat as a normalizing factor. This is really just a weighted average of the illuminance, where the weight is the number of seats (area covered divided by area per seat). Calculating weighted averages in this way, by using some auxiliary quantity (in this case area), is pretty common in physics.

The next thing I’ll need is the height of a given seat above the ground. This is specified by the model: I’ve constructed it so that the seat heights are given by a (relatively) simple formula,

The leading coefficient of \(\SI{0.001074}{ft.^{-1}}\) is chosen to be consistent with a central dome height of \(\SI{253}{ft.}\) (source), given that the dome spans a 90 degree arc. (Optional exercise for the reader: derive that.)

This integral is too complicated to be done symbolically, of course, but it’s not hard with a numerical algorithm, and the result is

Nice and simple. It even doesn’t have any units to worry about! Plugging this and the other numbers into the formula for illuminance, we get

Let’s see where we’ve gotten: plugging in the numbers for the Nokia 701 gives a paltry 9 lux! Remember, though, this is the illuminance received by the field and objects on it, not by the camera. We still have to account for how the light is attenuated and redistributed by reflection.

There are two effects to account for here. First, any material reflects only a fraction of the light it receives, given by a quantity called the albedo. Technically albedo is defined in terms of reflected and incident energy, whereas we’re using perceived brightness, but we can use the same values as a decent first approximation. Most of what the camera will be seeing is artificial turf, and the albedo of artificial turf is typically 5-10%.

Besides the drop in brightness caused by the reflection, we also have to account for the fact that not all the incoming light is reflected in the direction of the camera. As a model, I’ll take the turf to be a Lambertian reflector, which basically means that it reflects incoming light with equal luminance in all (upward) directions. Now, we already know that \(E_V = \iint L_V\cos\theta\uddc\Omega\). If the luminance \(L_V\) is equal in every direction, we can pull it out of the integral and find that, for a Lambertian reflector,

So, putting it all together, the luminance received by the field will be \(\frac{1}{\pi}\) times the illuminance it receives from the 71024 phones, which we’ve already calculated. Then the luminance reflected will be 5% of that. (I’m choosing a low value to offset the fact that this calculation is for the center of the field, the brightest part.) That luminance gets transmitted unchanged to the camera, where we integrate \(L_V\cos\theta\) over the camera’s field of view to get the illuminance delivered to the camera; this last integral brings in another factor which will be something less than \(\pi\). Let’s say it’s a factor of 2. The final expression is

To hit \(\SI{1345}{lx}\) on the camera, we need \(L_V A_\text{phone} = \SI{15200}{cd}\). For perspective, that’s about what you’d get from focusing 1700 lumens, the light output of a typical 100W incandescent bulb, into a 20 degree cone using a parabolic reflector. It’s also equivalent to the lower limit for a normal car headlight. So with a little over 35000 cars, you could illuminate the stadium, no external power needed!

If drive-in football ever becomes a thing, I totally called it.