Riding on water

Posted by David Zaslavsky on June 12, 2013 10:32 PM

— Comments

The Hyneman has a new line to add to his resume:

I kid, of course. Still, the Mythbusters’ demonstration of a motorcycle riding on water in last week’s episode was seriously cool. I have to admit, I didn’t expect it to work! But physics says otherwise — both the experiment, as we saw last week, and as I’m about to show you, the theory.

Underneath all the complicated fluid dynamical effects, a motorcycle can ride on water for much the same reason a speedboat does: it presents an upward slanted surface for water to bounce off of. For a speedboat, that surface is the hull; for a motorcycle, it’s the bottom of the wheels, especially the front wheel. But wheels are complicated. It’ll make things easier to start by examining the behavior of a speedboat-like slanted flat surface as it moves through water.

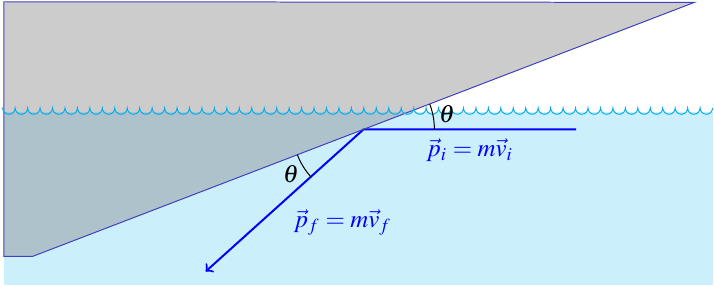
Conveniently, I’ve already done that calculation. It comes from another episode of Mythbusters a few years back, when they tried skipping a car across a lake. The calculation went like this: water molecules hit the lower surface of the car with a horizontal momentum $-mv \unitx$ and bounce off in a downward direction, with a final momentum $-mv(\unitx\cos 2\theta + \unity\sin 2\theta)$. I’m assuming the collision is elastic (just for simplicity; in reality, it’s not) so that the water molecules leave with the same speed they came in. They experience a change in momentum of

$$\Delta\vec{p} = -mv\unitx(\cos 2\theta - 1) - mv\unity\sin 2\theta$$

In a time interval $\Delta t$, the surface pushes through a mass of water equal to $\rho whv\Delta t$ — that’s density ($\rho$) times width ($w$) times height ($h$) beneath the water times length ($v\Delta t$).

$$\Delta\vec{p} = -\rho whv^2\Delta t[\unitx(\cos 2\theta - 1) + \unity\sin 2\theta]$$

Dividing by $\Delta t$ gives the force exerted on the water,

$$\vec{F}_\text{on water} = \lim_{\Delta t\to 0}\frac{\Delta\vec{p}}{\Delta t} = -\rho whv^2[\unitx(\cos 2\theta - 1) + \unity\sin 2\theta]$$

and the corresponding reaction force on the surface,

$$\vec{F}_\text{on surface} = \rho whv^2[\unitx(\cos 2\theta - 1) + \unity\sin 2\theta]$$

In my other blog post, I showed that this force is perpendicular to the surface (but it also makes sense if you just think about it). That takes care of the direction, and we can find the force’s magnitude using the Pythagorean theorem and the identity $\sqrt{(\cos 2\theta - 1)^2 + \sin^2 2\theta} = 2\sin\theta$ (check it), to write this as

$$\vec{F}_\text{surf} = -2\rho whv^2\unitn\sin\theta$$

where $\theta$ is the angle between the water’s impact direction and the surface.

Forces on a wheel

A motorcycle’s wheel differs from the undersurface of a boat in one important aspect: it’s curved. That just means the force exerted by the water will be different at different parts of the wheel.

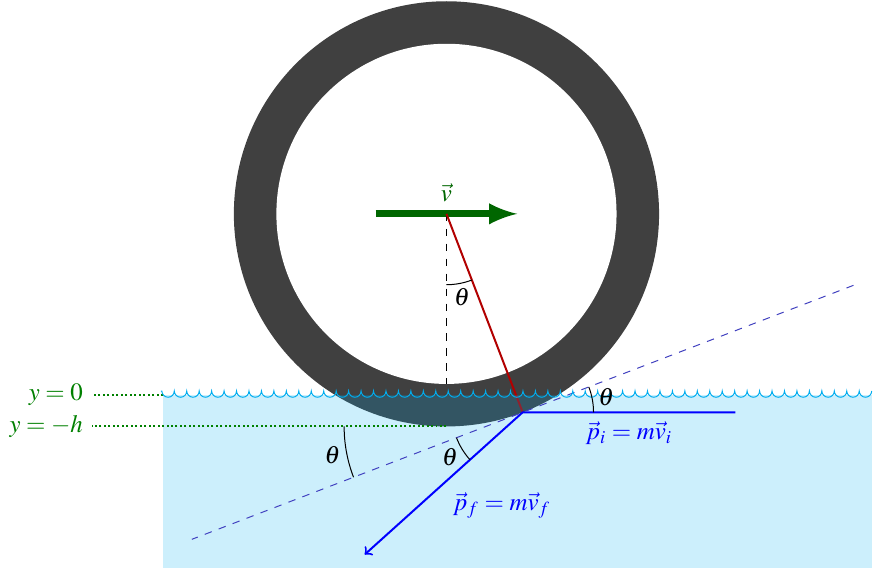
Consider a small wedge of angular width $\udc\theta$ at an angle $\theta$, as shown in the image above. It experiences a force $\udc\vec{F}$ in the direction

$$-\unitn = \unity\cos\theta - \unitx\sin\theta$$

and it spans a height

$$\udc y = R\sin\theta\udc\theta$$

Putting this into the equation for force on a surface, we get

$$\begin{align}\udc\vec{F} &= 2\rho w(R\sin\theta\udc\theta)v^2(\unity\cos\theta - \unitx\sin\theta)\sin\theta \\ &= 2\rho wRv^2(\unity\sin^2\theta\cos\theta - \unitx\sin^3\theta)\udc\theta\end{align}$$

This we can integrate over the range of $\theta$ where water is hitting the wheel, from $\theta = 0$, straight down, to $\theta = \acos\frac{R - h}{R}$, which is the direction to the point where the wheel meets the surface of the water. It works out to the slightly messy expression

$$\vec{F} = \frac{2\rho w}{3R^2}v^2\Bigl[-h^2(3R-h)\unitx + \bigl(h(2R-h)\bigr)^{3/2}\unity\Bigr]$$

representing the upward/backward force on the wheel due to its deflection of water.

Analyzing the motion

In this simplified model I’ve constructed, the motorcycle is subject to two forces: that of the water bouncing off the front wheel, given by the above formula, and gravity, given by good ol’ $\vec{F}_g = -mg\unity$. (I’m ignoring the effect of the back wheel, so this is going to be more like a motorized unicycle, but it gets the main point across.) So we can use Newton’s second law to get some equations of motion for the bike. In the horizontal direction,

$$F_x = m \udd{x}{t} = -\frac{2\rho w}{3R^2}\biggl(\ud{x}{t}\biggr)^2 h^2(3R-h)$$

and in the vertical direction,

$$F_y = m\udd{(-h)}{t} = \frac{2\rho w}{3R^2}\biggl(\ud{x}{t}\biggr)^2 \bigl(h(2R-h)\bigr)^{3/2} - mg$$

This is a messy enough set of differential equations that they can’t be solved analytically. But it’s not hard to find a numerical solution. I crunched the numbers using the GSL ODE integrators, so let’s look at some results!

Numerical results

Finding a specific numerical solution is a matter of setting values for the constants $m$, $\rho$, $w$, and $R$, and initial values for $h$, $\ud{h}{t}$, $x$, and $\ud{x}{t}$, and just letting the integrator run. Depending on the relationships between these values, the solution can behave in a couple different ways.

If the wheel’s initial submersion in the water, $h$, is large enough, or it’s dropping quickly enough, and if the wheel’s forward velocity is fast enough, we’ll get something that looks like this:

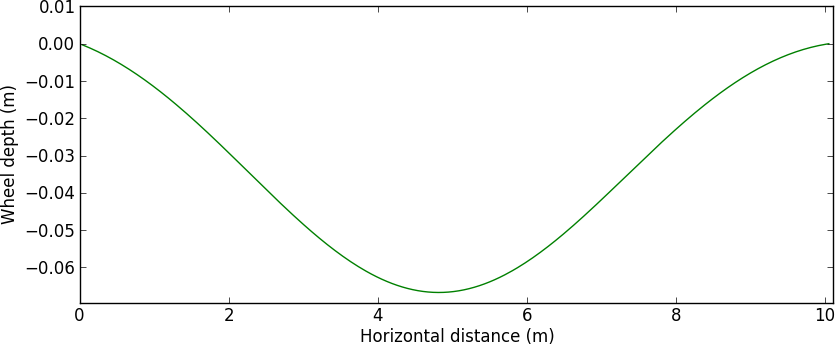
This shows the wheel bouncing out of the water, because the force exerted by the water against the wheel is strong enough to overwhelm gravity. Once the submersion depth makes it back to zero, the differential equations no longer apply — that’s the end of the solution shown in the graph. But then (since I’m pretending the motorcycle is actually a unicycle), projectile motion takes over and the wheel flies through the air until it hits the water again.

Each time the wheel bounces off the water, it loses some forward velocity. A loss of forward velocity translates to a loss of upward force, so eventually the wheel reaches a point where it no longer experiences enough force from the water to counterbalance gravity. When this happens, we get a graph that looks like this:

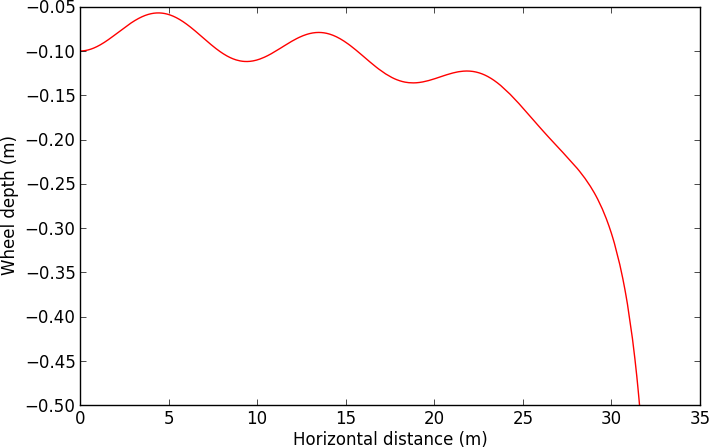
This plot is not to be trusted too much, because the whole model of water bouncing off the wheel becomes invalid once the wheel gets too deep, but the main point is clear: the thing sinks. Clearly, while it is possible to ride a motorcycle across water, there’s a limit to how far it will go.

Putting it all together, here’s a combined plot showing the bounces, free flights, and eventual sinking:

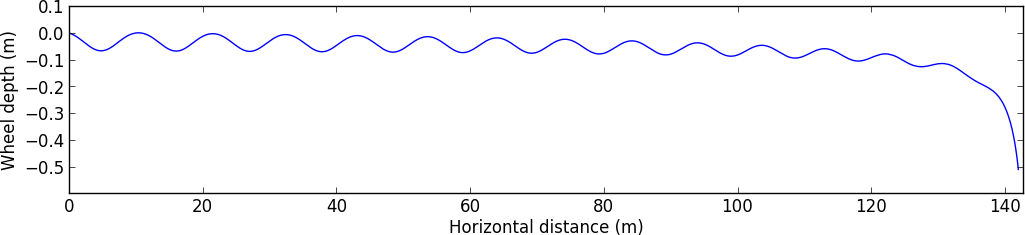
This was generated assuming a total mass of $\SI{200}{kg}$, an initial depth of zero (the wheel is right on the water’s surface), a vertical rate of fall of $\SI{0.27}{m/s}$ (semi-random choice), and an initial speed of $\SI{35}{m/s}$, just under $\SI{80}{mph}$. I’m guessing these values are roughly similar to those in Jamie’s actual last run over the lake on the motorcycle. You can see that the graph drops down to the bottom just over $\SI{140}{m}$ in — that’s $\SI{460}{ft.}$, which is not all that far off from the actual distance Jamie was able to ride in the show, about $\SI{300}{ft.}$ Considering all the other things that are going on that my model doesn’t account for (principally extra drag from the water spray and the back wheel, and rotations of the motorcycle), that’s not that far off!