The coolest thing since absolute zero
Posted by David Zaslavsky on — CommentsI’m a sucker for good (or bad) physics puns. And the latest viral physics paper (arXiv preprint) allows endless opportunities for them. It’s actually about a system with a negative temperature!
Negative temperature sounds pretty cool, but I have to admit, at first I didn’t think this was that big of a deal to anyone except condensed matter physicists. Sure, it could pave the way for some neat technological applications, but that’s far in the future. The idea of negative temperature itself is old news among physicists; in fact, this isn’t even the first time negative temperatures have been produced in a lab. But maybe you’re not a physicist. Maybe you’ve never heard about negative temperature. Well, you’re in luck, because in this post I’m going to explain what negative temperature means and why this experiment is actually such a hot topic. ⌐■_■
On Temperature
To understand negative temperature, we have to go all the way back to the basics. What is temperature, anyway? Even if you’re not entirely sure of the technical definition, you certainly know it by its feel. Temperature is what distinguishes a day you can walk around in a T-shirt from the day you have to bundle up in a coat. It makes the difference between refreshing lemonade and soothing tea. (If you drink your tea cold or your lemonade hot, I can’t help you.) Temperature is the reason you don’t put your hand in a fire. Basically, whatever temperature is, it has to allow you to tell things that feel hot apart from things that feel cold.
Now, if you think about some hot objects and some cold objects, like fire and ice, it might seem intuitive that hot things tend to have more energy than cold things. So you could define temperature as the average energy of an object. That definition actually works for the normal objects you interact with in your everyday life; it even works for a lot of less normal objects, like gases in extreme conditions. In fact in the kinetic theory of gases, temperature can be defined as being proportional to the average kinetic energy of the particles of the gas.
Here \(N\) is the number of particles and \(K\) is their kinetic energy, so \(\bar{K} = \frac{1}{N}\sum K\) is the average kinetic energy of the particles. \(n\) is a constant specific to the gas, \(k_B\) is the Boltzmann constant, and \(T\) is the temperature. Something analogous works for many solids and liquids, so in each case you can say that \(\bar{K}\propto T\): the temperature is related to the average kinetic energy.
But wait! Let’s go back and consider that definition of temperature a little more carefully, because that’s not the only one we could have come up with. All the hot objects you can think of do have a lot of energy, yes, but they also share a different characteristic: they will transfer a lot of energy to you if you touch them. Similarly, all the cold objects you can think of, in addition to having relatively little average energy, will transfer energy from you if you touch them. It might be hard to understand the difference at first, because for every object you can probably think of, having a lot of energy goes hand in hand with transferring a lot of energy, and similarly for small amounts of energy. So imagine a magic energy box which has a huge amount of kinetic energy, but for whatever reason, it always keeps that energy to itself. Even if you touch it, it won’t let any of its enormous “stockpile” of energy flow to your hand. Would it still be hot? Would it burn you to touch it?
As you probably guessed, no, it wouldn’t! Hopefully it makes sense that your sense of temperature is based on how much energy actually reaches your nerves, not how much happens to be sitting around next to them. That’s an example of a more general rule which you can apply to all sorts of physical systems: temperature is related to how readily a system transfers energy. Whatever definition we’re going to use for temperature, it has to turn out that energy tends to flow from an object with a higher temperature to an object with a lower temperature.
On Entropy and Multiplicity
There are a lot of different ways you could define temperature that at least seem to satisfy the criterion we’ve come up with. Showing why most of them either are not general enough, or just don’t work, would take a book, so I’m not going to do it here. I’ll just explain the definition that does work by way of a little example.

Imagine a colony of eight energy beings that live in two boxes marked out on a grid, as in the picture above. These are not the powerful interdimensional energy beings of science fiction; they’re just happy little energy packets who jump around randomly between their grid cells. Each way the energy beings can distribute themselves within some section of the grid — which could be the left box, or the right box, or both, etc. — is called a microstate of that section.
Let’s start by focusing on the left box. Suppose that at the beginning, there is one energy being in the left box. The picture shows one possible way this could happen, but you don’t know whether that’s the actual configuration or not; you only know that exactly one energy being is somewhere in that left box.
If you wait a little while, eventually one of two things will happen: either the energy being will jump out of the left box, or another energy being will jump into it from the right box. Finding out which box is hotter basically amounts to finding out which of these two options is more likely. If it’s the first, that means the left box tends to lose energy to its surroundings, making it hotter than the right box. On the other hand, if it’s the second option, that means the left box is cooler than the right one.
Microstates and probability: the ergodic principle
Hopefully it will at least seem intuitive that which option is more likely has something to do with how many configurations — microstates — it could end up in. For example, if an energy being jumps into the left box, there are more configurations than if one jumps out of the left box, and that suggests that a jump into the left box is more likely. But I’ll hold off on explaining exactly why that suggestion is correct until later. First we have to figure out which option has more possible final microstates.
Take the first option, where the lone energy being in the left box leaves it for the right box.
It’s easy to figure out how many microstates there are for the left box after this happens: one! With no energy beings, there’s only one possible arrangement: every cell in the grid is empty. So the number of microstates of the left box in this case is 1.
Now let’s go on to the second option, where an energy being jumps into the left box.
This one’s a little more complicated, because there are two energy beings that have to place themselves among the 16 grid cells. We can count the possible configurations with a little trick: imagine arranging the grid cells on a line, and then looking only at the edges between them.
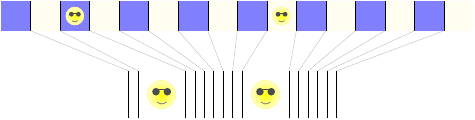
Each way of distributing the energy beings among the 16 cells corresponds to one way of ordering the 15 edges and 2 energy beings. And that, in turn, corresponds to one way of choosing 2 out of the 17 (that’s 15 + 2) positions to be occupied by energy beings, with the rest being occupied by edges. The number of ways to choose 2 out of 17 positions is
The 136 microstates make up a macrostate (note the one-letter difference), which is defined as the collection of all microstates with a given amount of energy. I’ll denote this macrostate \((2)_L\), because it has two units of energy, and it’s a macrostate of the box on the left (L). The number of microstates in the macrostate, in this case 136, is the multiplicity \(\Omega\), or in this specific case, \(\Omega_L(2)\). In the same notation, the macrostate for the first option, with no energy beings in the left box, would be \((0)_L\), and its multiplicity would be \(\Omega_L(0) = 1\).
If the left box were all there was to this setup, you could look at these two options, and say that there are 136 ways to get the second one and only one way to get the first, so clearly the second option is way more likely. But the left box isn’t all there is! There’s also a right box, and it can have its own configurations which affect the probabilities.
Consider the final macrostate of the first option, \((0)_L\). In this macrostate, there’s only one microstate for the left box, but it comes as a package deal with a macrostate for the right box, \((8)_R\), which has a large number of microstates of its own. We can figure out exactly how many using the same trick as before, but I’ll give it as a general formula this time: when you have \(N\) grid cells and \(n\) energy beings, the number of ways to arrange them is the number of ways to choose \(n\) of the \(n + (N - 1)\) positions to be occupied by energy beings, or
In this case there are 36 cells (so 35 edges) and 8 energy beings, giving 145 million possible configurations:
And what about the final state in the second option? With two energy beings on the left, there are six on the right. That means the left-box macrostate \((2)_L\) is paired with the right-box macrostate \((6)_R\), which has a multiplicity of
Clearly, the right box has a lot more microstates in the first option, when it has all eight energy beings, than in the second option, when it has only six. Each microstate of the left box is weighted by the number of microstates in the right box that can occur with it: the one left-box microstate in \((0)_L\) carries a weight of 145 million, whereas the 136 left-box microstates in \((2)_L\) carry a weight of only 4.5 million each.
All this talk about weighted probabilities is starting to get a little complicated, but fortunately, there’s a much easier way to think about it. We can put the (macro- or micro-) states of the left box and the states of the right box together, to get states of the combined boxes, and each of those is going to be equally likely. For example, when the left box has two energy beings and the right box has six energy beings, the left box has 136 microstates, and the right box has 4,496,388 microstates, for a combined total of \(\num{136}\times \num{4496388} = \num{611508768}\) microstates for the system as a whole. These constitute the macrostate \((2,6)\) — note that that’s a macrostate of both boxes, not just one. Similarly, there are \(\num{145008513}\) microstates where the right box has all eight energy beings, and they constitute the two-box macrostate \((0,8)\). Each microstate is just as likely as any other, so finding two energy beings in the left box is merely about four times as likely as finding none there, not 136 times as likely.
The assumption that all these individual microstates are equally likely, for an isolated system like the two boxes, is called the ergodic principle), and it underlies basically all of modern statistical mechanics.
The multiplicity distribution and the Second Law
Time for a recap: what have we learned so far? On average, the probability that a given macrostate will occur is proportional to its multiplicity. So in the example where the energy beings started in the macrostate \((1,7)\), with one in the left box and seven on the right box, they’re about four times as likely to transition into the macrostate \((2,6)\) than to transition into \((0,8)\), because \((2,6)\) has a higher multiplicity by a factor of about four.
The general rule to take away from that example should be clear: over time a system tends to work its way toward macrostates with higher multiplicities. This general rule is something you may have heard of before; it’s called the Second Law of Thermodynamics, and it’s usually stated like this:
The entropy of an isolated system tends to increase.
The entropy is just the logarithm of the multiplicity, times the Boltzmann constant:
so as a system works its way toward higher multiplicities, it’s also increasing its entropy.
Let’s think about this in the context of all the possible macrostates. First, here are all the relevant calculations:
| Macrostate | Energy | Multiplicity | Entropy (J/K) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Left | Right | Overall | Left | Right | Overall | Left | Right | Overall | Left | Right | Overall |
| (0)L | (8)R | (0,8) | 0 | 8 | 8 | 1 | 145,008,513 | 145,008,513 | 0 | 25.95×10-23 | 25.95×10-23 |
| (1)L | (7)R | (1,7) | 1 | 7 | 8 | 16 | 26,978,328 | 431,653,248 | 3.82×10-23 | 23.62×10-23 | 27.45×10-23 |
| (2)L | (6)R | (2,6) | 2 | 6 | 8 | 136 | 4,496,388 | 611,508,768 | 6.78×10-23 | 21.15×10-23 | 27.93×10-23 |
| (3)L | (5)R | (3,5) | 3 | 5 | 8 | 816 | 658,008 | 536,934,528 | 9.26×10-23 | 18.50×10-23 | 27.75×10-23 |
| (4)L | (4)R | (4,4) | 4 | 4 | 8 | 3876 | 82,251 | 318,804,876 | 11.41×10-23 | 15.63×10-23 | 27.03×10-23 |
| (5)L | (3)R | (5,3) | 5 | 3 | 8 | 15,504 | 8436 | 130,791,744 | 13.32×10-23 | 12.48×10-23 | 25.80×10-23 |
| (6)L | (2)R | (6,2) | 6 | 2 | 8 | 54,264 | 666 | 36,139,824 | 15.05×10-23 | 8.98×10-23 | 24.03×10-23 |
| (7)L | (1)R | (7,1) | 7 | 1 | 8 | 170,544 | 36 | 6,139,584 | 16.63×10-23 | 4.95×10-23 | 21.58×10-23 |
| (8)L | (0)R | (8,0) | 8 | 0 | 8 | 490,314 | 1 | 490,314 | 18.09×10-23 | 0 | 18.09×10-23 |
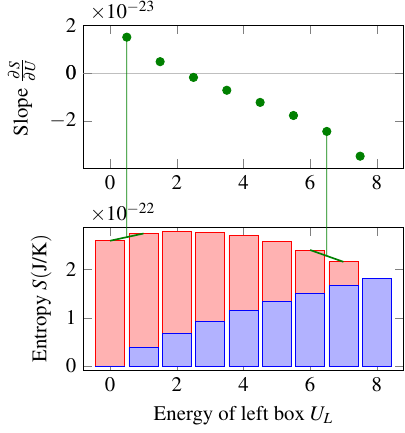
That data goes into the following graph, which shows the multiplicity of each macrostate. On the horizontal axis is the amount of energy in the left box.
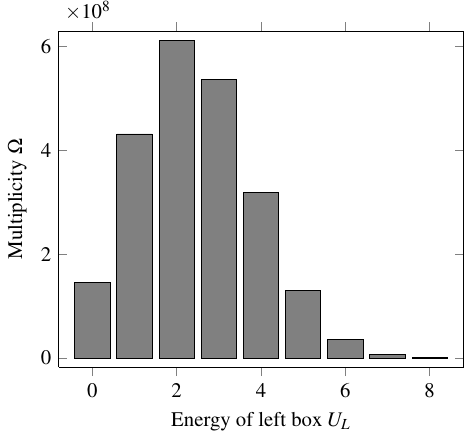
Saying that the system of energy beings tends to transition toward higher multiplicity, or higher entropy, is equivalent to saying that, over time, it will work its way up the slope of the graph. In this case, that means:
- When multiplicity is increasing with the energy of the left box, \(\pd{\Omega}{U_L} > 0\), the left box is cooler than the right box, because it will tend to take on more energy from the right box
- When multiplicity is decreasing with the energy of the left box, \(\pd{\Omega}{U_L} < 0\), the left box is hotter than the right box, because it will tend to give off more energy to the right box
- When multiplicity is neither increasing or decreasing with energy, \(\pd{\Omega}{U_L} = 0\), the two boxes are at the same temperature
So the temperature difference is inversely related to \(\pd{\Omega}{U_L}\)! This will be the basis of the quantitative definition of temperature.
Temperature
At this point, we know that temperature can be written as some (inverse) function of the slope \(\pd{\Omega_E}{U_O}\). Here the subscript O stands for “object”, S would stand for “surroundings”, and E stands for “everything” (the object and surroundings). In the energy being example, the left box would be the object and the right box would fill the role of the surroundings. But there are a few problems with this.
First of all, we shouldn’t have to calculate the multiplicity of everything to figure out whether an object is hotter than its surroundings. In the case of the energy beings in the boxes, it wouldn’t be too hard, but what about real objects? Should we have to count the multiplicity of the entire universe to measure a temperature? I don’t think so. We should be able to find some alternate definition of temperature that depends only on the properties of the object itself.
OK, fine, so what about making temperature a function of \(\pd{\Omega_O}{U_O}\)? Unfortunately, there’s a problem with this, too, but it’s a little more subtle. Remember that the second law of thermodynamics tells us that systems tend to shift toward higher-multiplicity microstates until they wind up at the peak of the multiplicity graph. When this happens, the object should be at the same temperature as its surroundings, because they’re not going to exchange energy anymore. If we defined an object’s temperature as being related to \(\pd{\Omega_O}{U_O}\), then that means
should hold at the multiplicity peak. But it doesn’t. We can see this because, at a local maximum of the multiplicity graph, the slope of the graph is zero; that is,
The overall multiplicity is the product of the multiplicities for the object and surroundings, \(\Omega_E = \Omega_O \Omega_S\). Plugging that in, we get
And whenever the object’s energy changes, the energy of the surroundings changes by the opposite amount, so that total energy is conserved. That means \(\pd{}{U_O} = -\pd{}{U_S}\), so
This isn’t the same condition as \(\pd{\Omega_O}{U_O} = \pd{\Omega_S}{U_S}\); it’s not even equivalent! So \(\pd{\Omega_O}{U_O} = \pd{\Omega_S}{U_S}\) does not hold at the peak of the multiplicity graph.
Fortunately, the condition that does hold at the peak suggests a solution. If you divide that last equation through by \(\Omega_S\Omega_O\) and move one term to the other side, you get
So if we define temperature as being inversely related to \(\frac{1}{\Omega}\pd{\Omega}{U} = \pd{\ln\Omega}{U}\), everything works! In fact, if we multiply this by the Boltzmann constant, it just becomes \(\pd{S}{U}\). That’s why entropy is defined the way it is: it goes right into the definition of temperature.
Negative temperatures
The last thing to do is to figure out just what kind of inverse relationship exists between temperature \(T\) and the slope \(\pd{S}{U}\). In some sense, it doesn’t really matter, because picking a different relationship just rescales the temperature differences between different objects; it doesn’t change whether something has a higher or lower temperature. You could pick any inverse relationship and invent a way to do thermodynamics with it.
In practice, the definition we actually use is
This definition has the advantage that it agrees with the results from kinetic theory, like the ideal gas law. In particular, using this definition, when a substance heats up, the change in its volume is proportional to the change in temperature. This means that you can construct a liquid or gas thermometer with a linear scale.
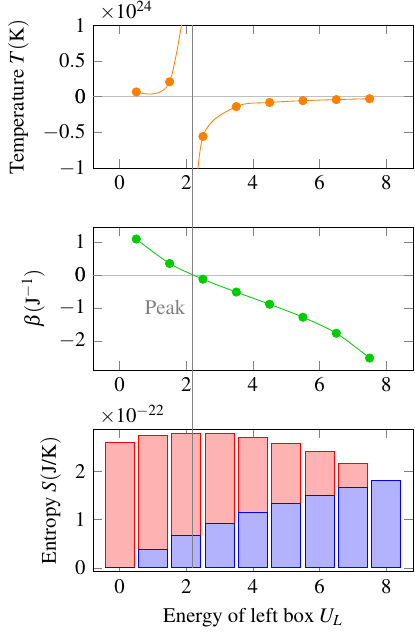
However, this definition has one interesting quirk. Look at the graph of entropy vs. energy. As long as you’re on the left of the peak of the graph, entropy increases with energy, so the temperature, as the reciprocal of the slope, is positive. But to the right of the peak, the entropy decreases with energy, so the slope is negative, and the temperature is negative! This is what it means to have a negative temperature: that as you add energy, the entropy gets smaller and smaller. Whenever the graph of entropy vs. energy has a peak and then drops back down to zero, the temperature will be negative at higher energies.
Because it’s kind of strange to have the temperature switch from positive to negative as energy increases, physicists sometimes use an alternative definition,
This \(\beta\) doesn’t actually measure temperature, because as you can tell, it’s directly, not inversely, related to the slope of the entropy-energy graph. So it might be more accurate to call it “coldness,” but for now it just has the unimaginative name of “thermodynamic beta”. Anyway, \(\beta\) decreases smoothly from infinity to negative infinity as you move through the entire range of energies allowed for the system. In that sense, it’s kind of a more natural way to characterize how objects interact thermally. It shows that there’s really nothing fundamentally strange about negative temperature; in a sense, it’s just a historical accident that the common definition of temperature runs out of numbers (hits infinity) too soon, and using \(\beta\) is how we can extend the scale to encompass all possible temperatures.
Here’s a graph showing how these two quantities behave for our energy beings in boxes:
Creating Negative Temperature in an Optical Lattice
The paper itself was published a few days ago in Science. It describes how a group of seven German physicists constructed a system with a negative temperature by placing potassium atoms in an optical trap.
Optical traps, or more precisely optical lattices, are a common device in low-temperature physics experiments. Basically, an optical lattice is a standing electromagnetic wave created by shining two laser beams through each other in opposite directions. You can do this in more than one dimension to get a 2D or 3D trap. The interference between the laser beams creates a periodic potential energy function, a series of hills and valleys that can trap low-temperature particles in a given location in space. By adjusting the phases, relative angles, and strengths of the laser beams, you can do all sorts of manipulations on the lattice, changing around the locations of the potential minima and trapping or releasing atoms during the course of the experiment.
For this particular experiment, the energy of a particle in the lattice can be calculated from this expression:
The first term represents the quantum mechanical version of the kinetic energy of a potassium atom moving from one site in the lattice to another. The second term represents the energy of the interaction between different atoms sitting in the same lattice site, which can be attractive or repulsive, and the third term represents the potential energy each of these atoms has by virtue of being trapped in the lattice, which can be negative or positive (the latter is like “anti-trapping”, it repels atoms from a specific site).
In order to create a negative-temperature state, the most important thing the scientists needed to do was find a way to place an upper limit on each of these three types of energy. Remember, having a negative temperature requires that the number of available microstates decreases as the energy rises, and if you can set up a maximum energy where the system runs out of microstates, that’s a surefire way to make the entropy decrease as it gets closer to that maximum. The optical lattice naturally places an upper bound on the kinetic energy, but for the other two terms, the researchers found that it’s necessary to arrange for the interactions between atoms to be attractive (rather tha repulsive) and use an anti-trapping potential in order to get that upper limit.
Here’s what they saw:
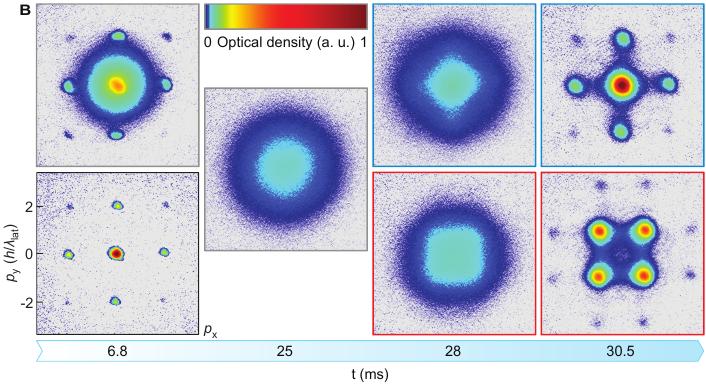
This figure from the paper shows snapshots of where the potassium atoms are clustering in the lattice in two runs of the experiment, one on top and one on the bottom, with time increasing from left to right. At the beginning of the experiment, the left column, you can see that the atoms are clustering in the valleys of the optical lattice. As time goes on, in the top run, the atoms stay roughly in their original positions. But in the bottom run, you can see that the points where there are a lot of atoms change. They’ve moved from the valleys of the potential to the peaks! That shows the upper bound on energy which is necessary for a negative temperature.
To be clear, at this point, this experiment is still very much basic science. All the authors have shown is that it’s possible to make a stable negative-temperature state of a few atoms, with the energy coming from motion instead of spin (which is how negative temperature states have been created in the past). But it’s possible that this could be turned into some larger-scale technology. If so, negative temperature materials could be used to construct highly efficient heat engines. And as the authors point out in the paper, negative temperature implies negative pressure as well, which could be a way of explaining the cosmological mystery of dark energy. So I’ll be quite interested to hear about how this idea develops.
