Bullet Fired vs. Bullet Dropped

Posted by David Zaslavsky on October 10, 2009 12:05 AM — Edited May 1, 2012 2:40 AM

— Comments

With their season premiere this week, the Mythbusters are testing a classic physics story, so of course I had to comment on it. The myth in question is that if you fire a bullet from a gun held horizontally, it will hit the ground at the exact same time as a bullet dropped without any horizontal motion at all.

Of course, in the mind of any physicist, this is no myth at all — the laws of physics that tell us this should happen are so well established that they’re almost beyond question. Specifically, it’s the linear independence of orthogonal vectors, which means that components of motion that are perpendicular to each other, like gravity (vertical) and constant velocity (horizontal), don’t get in each other’s way. You can split the motion of the bullet into two perpendicular components and analyze each one separately. This is, in fact, one of the first things students learn in an introductory physics class: analyzing the motion of a fallen or thrown object. The equations $x = v_{0x}t$ and $y = -\frac{1}{2}gt^2$ work for both the fallen bullet and the dropped bullet, just with $v_{0x} = 0$ in the latter case. But that velocity doesn’t make any difference at all to the vertical motion, since $v$ doesn’t appear in the equation for $y$ at all.

Unfortunately, (practically) nothing in real-world physics is really that simple. In reality, we have air resistance to deal with. Air resistance slows down a speeding bullet, and so you’d think that it would hold the fired bullet back, so that the dropped bullet would hit the ground first. But wait! The dropped bullet is also moving through the air, and it experiences air resistance as well. So does that mean that they would hit the ground at the same time after all?

The drag force on an object moving through a fluid can be calculated as

$$F_D=\frac{1}{2}\rho v^2 A C_D$$

where $\rho$ is the density of the fluid, $v$ is the object’s velocity, $A$ is its cross-sectional area, and $C_D$ is the drag coefficient, which is typically on the order of 0.1 for streamlined shapes or 1 for rounder or blockier shapes. Wikipedia reports $C_D \sim 0.295$ for some bullets so let’s go with that. The first thing to notice is that this formula depends on velocity squared — it’s non-linear. That means that when drag force is involved, the horizontal and vertical components of velocity may not be independent anymore.

Drag force always acts antiparallel to the overall velocity of a moving object. So if the bullet is moving straight horizontally, as it starts out, the drag force will also be horizontal, but as the bullet’s trajectory tilts downward, the drag force will angle upward to remain antiparallel. The horizontal and vertical components of the drag force are

$$\begin{aligned}F_{Dx} &= \frac{1}{2}\rho v^2 A C_D \frac{v_{x}}{v} \\ F_{Dy} &= \frac{1}{2}\rho v^2 A C_D \frac{v_{y}}{v}\end{aligned}$$

and including that effect modifies the equations of motion to

$$\begin{aligned}x(t) &= v_{0x} t - \frac{\rho A C_D}{4m}v(t) v_{x}(t) t^2 \\ y(t) &= -\biggl(\frac{g}{2} + \frac{\rho A C_D}{4m}v(t) v_{y}(t)\biggr) t^2\end{aligned}$$

Clearly, this is no longer a simple set of equations. You can’t solve it exactly, but you can simulate it on a computer.

I set up a simulation of the track defined by these equations, using the Open Source Physics toolkit to do the calculation and rendering. In the show, Adam and Jamie said that they found the two bullets (fired and dropped) hitting the floor within about 36 milliseconds of each other. What the simulation can tell us is whether air resistance accounts for that difference. So does it? Well, here’s the simulated result:

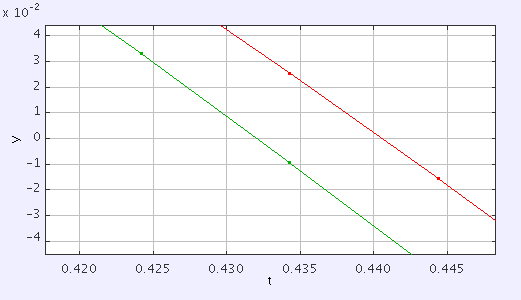
This graph is zoomed in closely on the point where both bullets would be hitting the floor (that would be the 0 on the vertical axis). The green track represents the dropped bullet and the red track represents the fired bullet. According to this output, the dropped bullet in the simulation hits the ground after falling for $\unit{432}{\milli\second}$ and the fired bullet hits the ground after failling for slightly under $\unit{441}{\milli\second}$ — a difference of only $\unit{9}{\milli\second}$, about a quarter of what the Mythbusters observed.

So, does this mean that a dropped bullet and a fired bullet actually don’t hit the ground at the same time? Actually, we really can’t tell based on the Mythbusters’ single experiment and one simple simulation. $\unit{9}{\milli\second}$ is a pretty small time compared to the total flight time of the bullets, and if we wanted to be able to confidently compare the simulation’s result to reality, we’d need to have a much more accurate model of the forces acting on the bullet in flight. And even if our simple model is reasonably accurate, there are only a few tens of milliseconds left to be accounted for by other factors. That’s not very much. Everyday devices like the gun and the drop rig used in the experiment just aren’t designed to activate with that level of precision, so it’s easy to imagine that some sort of mechanical randomness could introduce a fraction of a second’s delay one way or the other, enough to account for the discrepancy between the experiment and the simulation. It would have been great if the Mythbusters took the time to repeat their shot to try to eliminate statistical errors from the data, but the next 20 trials probably aren’t such great television.