How the Mythbusters skipped a car

Posted by David Zaslavsky on December 28, 2009 12:23 AM — Edited June 12, 2013 5:39 AM

— Comments

On the last episode before breaking for Christmas, the Mythbusters build team undertook the slightly ambitious project of skipping a car across a pond, as shown in the movie Cannonball Run. At first this probably seems like a ridiculous thing to try — of course, on Mythbusters, what isn’t? But this one actually worked. Here’s a look at the rather interesting physics behind it.

As Jesse explained on the show, there are basically two physical principles that allow you to skip a stone (or a car) across water: the spin, and the reaction force of the water. This isn’t buoyant force, like they’ve dealt with on previous shows; if buoyancy alone were the only thing pushing up on the stone, it’d float. Stones don’t float. (Neither do cars.) The force that keeps a stone skipping across the water is related to its speed. Spin and speed, that’s the magic formula.

First, the spin. Any spinning or rotating object has angular momentum, which is like a rotational equivalent of linear momentum: roughly speaking, it measures how difficult it is to change the object’s motion. Objects with a lot of momentum are either very massive or moving very fast, or both, and in either case they’re not going to change that motion easily. The corresponding formula for linear momentum is

$$\vec{F} = \ud{\vec{p}}{t}$$

showing that the rate of change of momentum is equal to the force, and for angular momentum,

$$\vec{\tau} = \ud{\vec{L}}{t}$$

showing that the rate of change of angular momentum is equal to the torque. Unless you have something pushing very hard on it, a rapidly spinning object is not going to change its spin by any significant amount in the short time involved in skipping across a pond. What’s especially important here is that spin is a vector; it has a magnitude and a direction, and both of them are going to remain effectively constant. So in addition to continuing to spin at the same rate, a skipped stone will keep its spin axis pointing in the same direction, like a gyroscope. (Just kidding, try this) This is the purpose of spinning a stone when you skip it, so that it maintains the same orientation even as it gets jostled by the water. (It wasn’t necessary to spin the car because its large mass keeps the water from flipping it over.)

The big question, of course, is why a stone (or car) is able to bounce off the surface of the water at all. As you might guess, this has to do with the speed. Water bouncing off the bottom of the stone exerts an upward force on it, and the faster the motion, the larger the force. Working out a formula for this force is, if not outright difficult, a little tricky. We need to shift our perspective and imagine ourselves moving along with the stone at some particular instant — basically, instead of thinking about the stone hitting water at a velocity $\vec{v}$, we consider a molecule of water hitting the stone with the same speed but in the opposite direction, $-\vec{v}$.

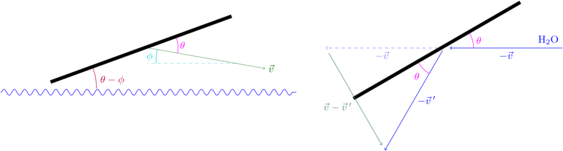
Suppose the molecule bounces off the stone elastically; that is, it keeps the same kinetic energy it had before the collision. That means it’s going to have the same speed. Only the direction of the velocity changes, because the component of velocity perpendicular to the surface gets reversed; it’s just like light bouncing off a mirror, and just like light, the angle of incidence will equal the angle of reflection. From the diagram, we can work out the final velocity of the water molecule,

$$-\vec{v}' = -v\cos(2\theta)\unitx - v\sin(2\theta)\unity$$

and then the difference

$$\vec{v} - \vec{v}' = v[1 - \cos(2\theta)]\unitx - v\sin(2\theta)\unity$$

This quantity is important because when you multiply it by the mass of the water molecule, $\mu_w$, you get the momentum change of the water,

$$\Delta \vec{p}_w = \mu_w\bigl[v\bigl(1 - \cos(2\theta)\bigr)\unitx - v\sin(2\theta)\unity\bigr]$$

which is precisely equal and opposite to the change in momentum of the surface caused by this collision,

$$\Delta \vec{p} = -\mu_w\bigl[v\bigl(1 - \cos(2\theta)\bigr)\unitx - v\sin(2\theta)\unity\bigr]$$

The next step is to figure out how many molecules are going to bounce off the surface per unit time. That’s just the number density of molecules, $n$, times the volume the surface passes through in a unit time $\Delta t$, which is $\vec{A}\cdot\vec{v}\Delta t$. The dot product takes the component of velocity parallel to the area’s normal vector, and it just works out to $n A v \cos(\pi - \theta) \Delta t$, or $n A v\sin\theta \Delta t$. Multiplying this by the change in momentum per molecule, we get

$$\Delta \vec{p} = -\mu_w n A v\sin\theta \Delta t\bigl[v\bigl(1 - \cos(2\theta)\bigr)\unitx - v\sin(2\theta)\unity\bigr]$$

But notice that $\mu_w n = \rho$, the mass density of the water. Dividing both sides by $\Delta t$, we get the force,

$$\vec{F} = \frac{\Delta \vec{p}}{\Delta t} = -\rho A v^2\sin\theta\bigl[\bigl(1 - \cos(2\theta)\bigr)\unitx - \sin(2\theta)\unity\bigr]$$

Hmm, this factor $\rho A v^2$ looks familiar… we’ve just more or less rederived the equation for aerodynamic drag that pops up rather frequently in the Mythbusters’ experiments.

There’s one last thing to do with this expression before we can go on plugging in numbers. In the reference frame where the stone is at rest, we’ve been working in a rotated coordinate system, chosen so that the velocity $\vec{v}$ points directly along the $-\unitx$ axis. But we want to find the vertical force that holds the stone up — that’s vertical in the “stationary” reference frame, where the stone is moving and the water is not. Of course, I could just multiply the force we got by the appropriate rotation matrix. But instead I can use a little trick: I’ll express all the vectors in terms of the directions defined by the problem itself. What I mean is, instead of writing $\unitx$, use $\unitvec{p}$, and instead of $\unity$, I’ll invent a vector $\unitvec{\eta}$ which points perpendicular to $\unitvec{p}$ by definition. Unlike $\unitx$ and $\unity$, these vectors won’t arbitrarily change their orientation when we switch coordinate systems. I can write the force as

$$\vec{F} = -\rho A v^2\sin\theta\bigl[\bigl(1 - \cos(2\theta)\bigr)\unitvec{p} - \sin(2\theta)\unitvec{\eta}\bigr]$$

and from a drawing of the overall setup, I can easily tell that

$$\unitvec{p} = \cos\phi\unitx - \sin\phi\unity$$

and

$$\unitvec{\eta} = \sin\phi\unitx + \cos\phi\unity$$

Plugging in and simplifying,

$$\vec{F} = -\rho A v^2\sin\theta\bigl[\bigl(1 - \cos(2\theta)\bigr)(\cos\phi\unitx - \sin\phi\unity) - \sin(2\theta)(\sin\phi\unitx + \cos\phi\unity)\bigr]$$

which conveniently reduces down to

$$\vec{F} = 2\rho A v^2\sin^2\theta[\cos(\theta - \phi)\unity - \sin(\theta - \phi)\unitx]$$

If you look back at the diagram above, you’ll notice that this vector describes a force which points perpendicular to the surface of the object being skipped — not to the surface of the water! I’ll note that we could have arrived at the same conclusion using the coordinate-free form of the equation,

$$\vec{F} = \rho A (\unitn\cdot\vec{v})^2\unitn$$

where $\unitn$ is the unit normal to the surface. The derivation is more or less the same as above, if you make some effort to represent all the vectors in terms of $\vec{v}$ and $\unitn$ from the beginning.

Anyway, now that we have an equation, it’s time to calculate some numbers. Unfortunately, this is going to be the difficult part. It’s easy enough to estimate $v$, that’s just the speed of the car, and $\rho = \unit{1000}{\frac{\kilo\gram}{\meter^3}}$ is the density of water, but the other values depend on the exact shape and trajectory of the car, which are a completely separate issue from the calculation I’m talking about today. For our purposes, I’m just going to make some guesses based on what I remember seeing in the show.

First, let’s consider the Mythbusters’ attempt to replicate the circumstances of the movie: a (makeshift) luxury car flying off an 8 foot ramp at $\unit{50}{\mileperhour}$. This car spun around in the air and hit the water nose-down, so the surface of interest is the front grill, which probably has an area around $\unit{1}{\meter^2}$. We can get an approximate measurement of $\theta - \phi$ by looking at the video capture of the car (or perhaps by calculating it, but that’s a topic for another day). Unfortunately, I don’t have this video. So I’m just going to guess. At the point when the car hits the water, it’s probably inclined by about $\unit{70}{\degree}$. $\theta$ is a bit harder to determine, but it has to be pretty small, probably not more than $\unit{20}{\degree}$. With these numbers, the force works out to $\unit{20000}{\newton}$, or $\unit{4500}{\pound}$. That’s a lot of force! Enough to support the full weight of the car, in fact. But then again, as the car’s speed drops, so does the force, which means that the drag force isn’t going to last long enough to make our car float. It just means it slows down fast.

Now consider the second car jump, the one without the ramp where the car actually made it across the pond. This time the speed was higher, $v = \unit{100}{\mileperhour}$, but more importantly, the car didn’t spin around in midair, so it hit the water more or less flat, with a fairly large horizontal velocity. That’s significant for two reasons: first of all, the surface of interest here is not the front of the car, but the bottom, and there is a lot more surface area on the bottom of the car that could potentially be contributing to the drag force. But more importantly, since the force acts perpendicular to the surface, in this case it’s pointing almost directly upward — not antiparallel to the car’s velocity! So instead of slowing the car down, this force pushes it back up out of the water, causing it to skip. It’s not particularly easy to estimate the angles $\theta$ and $\phi$, but knowing that they’re both really small,

$$\vec{F}\cdot\unity \sim 2(\unit{1000}{\frac{\kilo\gram}{\meter^3}})(\unit{1}{\meter^2})(\unit{100}{\mileperhour})^2\sin^2\theta\cos(\theta - \phi) \approx \snunit{2}{6}{\newton}\sin^2\theta$$

That amplitude is about $\unit{450000}{\pound}$, so even with $\theta$ as small as about $\unit{4}{\degree}$, it’ll be enough force to completely counteract the weight of the car and bounce it back up into the air.