This is one of those really cool things that I’ve often wondered about: can you really shoot a gun out of an outlaw’s hand? Last week on Mythbusters, Adam and Jamie decided to test it out. Sure, it’s not the kind of thing you’d think would be easy (or safe) — unless you have access to that classic Mythbusters creativity. Their first idea involved a Velcro-like gripping arm to hold the gun, and although it may not be clear just how exactly that compares to a real hand, they obtained some interesting results from comparing the different gripping positions.

Anyone who’s ever tried to pry an object out of somebody’s hand knows that the easiest way to do it is to twist it to apply stress on the thumb, the weakest point of the grip — not just to hit it as hard as possible. And whenever an object is twisting or rotating, the operational physical principle is torque, the rotational analogue of force. Torque can be calculated from the formula

but in most simple cases, we can identify an axis of rotation and then calculate the torque around that axis as

Here \(r\) is the radius of rotation, the distance from the axis to the point at which the force is applied in the direction perpendicular to the force.

For a gun in an outlaw’s hand, the easiest axis of rotation is pretty clear: it runs up and down along the handle of the gun. His fingers wrap around the handle, holding it more or less in place (as long as he’s able to hold on to it), but there’s not much other than friction to prevent the gun from rotating around while the handle stays in his hand. According to the formula \(\tau = rF\), then, you can get a higher torque by shooting a point on the gun that’s further away from this rotation axis. This is exactly why the “hostage position” on the show was the easiest one to disarm: you’re shooting at a side view of the gun, which allows you to hit it near the business end of the barrel, far away from the axis of rotation. \(r\) in this case can be up to the length of the gun, maybe \(\unit{15-20}{\centi\meter}\) for the type they were using on the show.

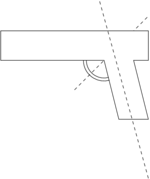
Of course, Adam and Jamie also tested two other positions, the “draw position” and the “shooting position.” Neither of these gives you a side view of the gun, so if you hit it, you’re shooting right in line with that axis of rotation that runs through the handle. This means that you won’t be able to twist the gun around that axis. But there are other ways it can twist; specifically, the gun can rock back and forth in the outlaw’s hand, and with enough force from the bullet, it can rock right out of his grip. The same rule about torque applies, namely that the further away from the axis of rotation (which now runs through the trigger hole, more or less) you hit, the more torque the bullet can apply. And that’s indeed what Adam and Jamie found: in the “draw position,” when you get a top view of the gun, you can again hit it up to a barrel length away from the axis, making it hard to hold on to, whereas in the “shooting position” you’re facing the smallest possible target presented by the gun and are forced to hit it nearly on-axis. This tends to knock the outlaw’s hand back but not really dislodge the gun.

Besides the radius from the rotation axis, the amount of torque exerted by a bullet is also influenced by the force the bullet can impart, and that in turn depends on how the bullet collides with the gun. From the high-speed footage in the show, we saw that the bullets flew apart into a lot of little pieces when they hit the gun, and the pieces spread out in all different directions. This is what we in physics call an inelastic collision (an elastic collision would have the objects involved just bouncing off each other). Inelastic collisions can be quite difficult to analyze, because not only are there many different pieces to keep track of, but those pieces could have a range of different velocities depending on how much energy is lost to heat and sound. Still, we can make some reasonable-sounding guesses.

Suppose, for instance, that after the collision, all the pieces of the bullet have the same forward velocity \(v\), and the gun’s forward velocity is some possibly different forward velocity \(u\). Then the total post-collision momentum is

where I’ve indicated that it has to be equal to the pre-collision momentum \(m_\text{bullet} v_0\). Also, we can compare the total energy before and after the collision,

Putting these together, we get

which translates to

(I used a computer to simplify that, but you could work through it by hand if you wanted to) This places an upper limit on the momentum of the gun after the collision. And this, in turn, is useful because the force is given by

(this is a rough approximation, but it lets me avoid relying on information I don’t have) We can estimate \(\Delta t\), the time over which the momentum change takes place, to be approximately the amount of time it takes the bullet to travel its own length,

and putting all this together,

So we’ve calculated a rough upper bound for the amount of force that you’d feel from a bullet hitting your gun, and knowing the radius from the rotation axis, we can use \(\tau = rF\) to calculate the maximum torque.

Why did I do that? I’d like to compare the actual impact from the bullet with the gun-shaped paddle target that Adam built to test whether he’d be able to hold on to a gun. According to Jamie, for that experiment they chose the mass and speed of the baseball bat so that it would have the same kinetic energy as a bullet. But I think they should have been comparing torque. (Then again, that calculation makes for lousy entertainment, I suppose it’s too much to expect them to do it on the show ;-)

Let’s start with the torque delivered by a real bullet. Obviously the numbers involved will vary from one type of bullet (and gun) to another, but Jamie quoted values of \(m_\text{bullet} = \unit{15}{\gram}\) and \(v_0 = \unit{613}{\mileperhour}\) on the show, so let’s go with that. I’ll have to estimate some other values, \(m_\text{gun} \sim \unit{1}{\kilo\gram}\) and \(l_\text{bullet} \sim \unit{1}{\centi\meter}\). (if someone can identify the type of bullet and gun they used on the show so I can get better values, please let me know!) Plugging these numbers in, we get

Whoa. That’s a lot of force. But still, we’ve just calculated an upper bound, so the real amount of force could definitely be a lot less.

Anyway, on to compare with the bat. Since the inequality from above was derived for a bullet and a real gun, we’ll need to check and see how well it applies to a bat and a target… as it turns out, there really isn’t much that needs to change. Everything I said about conservation of momentum and energy was completely general, so it applies equally well to both situations; we just need to come up with a new estimate for how long the collision between the bat and the target takes. Unfortunately, trying to do so analytically would be worthy of an entire post itself (probably longer than this one), and it depends on a lot of factors that we really have no information about, such as how tightly Jamie was holding the bat. I’m just going to make a guess that the collision occurs within the space of about \(\unit{5}{\centi\meter}\). Then plugging in that for \(l_\text{bullet}\), \(m_\text{gun} = \unit{1}{\kilo\gram}\) again, \(m_\text{bullet} = \unit{800}{\gram}\), and \(v_0 = \unit{85}{\mileperhour}\), we get

which, while still a lot of force, is a whole order of magnitude less. You might object that the target-paddle-toy Adam built may have been a lot lighter than a real gun, but it turns out that that further reduces the force. So these numbers are strongly indicating that the torque from a real bullet impact on a real gun is a fair amount more than from a baseball bat hitting a paddle.

Just one problem: that’s not what we saw on the show! Toward the end, when the Mythbusters tried Jamie’s idea of holding a gun to see if they could withstand the shock when it was fired, Adam was able to hold on to the gun in all three positions, whereas when he tried the paddle… well, did you see the look on his face? (If you didn’t: it was painful) There are a few possible explanations I can think of. First of all, Adam himself said that the “training” he got from the baseball bat experiment may have better equipped him to hold on to the gun. Also, a lot of uncertainty comes in from estimating the distance over which each collision takes place, \(l_\text{bullet}\). Those numbers could have been off by an order of magnitude or so, especially in the case of the bat, and that could mean that the forces were not so dissimilar.

I suspect, though, that the major factor might be one particular difference between a baseball bat and a bullet that I haven’t really accounted for: the bat has a person on the other end, and that person can keep applying extra force throughout the collision. This essentially increases the period over which the force is applied, as well as increasing its magnitude, and that can definitely make a big difference. If you don’t believe it, try opening a door by repeatedly throwing a baseball at it. (On second thought: don’t try this at home) Unless the door is particularly well balanced, it doesn’t budge very much, because the baseball, like a bullet, can only apply a limited impulse. Compare that with how easy it is to open a door with a push of your hand — not because you push with a larger force, but because you can sustain it even as the door starts to move away from you.

I guess this means that if you’re ever in the situation of having to disarm someone without hurting them, opt for the baseball bat ;-P But seriously: as found on the show, bullets just aren’t going to do the job.