Id: 125

(I’ve had some technical problems that kept me from getting this post out on time, but better late than never!)

On the episode of Mythbusters aired a couple weeks back, Kari, Grant, and Tory set out to test the myth that if you have a car driving forward at, say, 60 miles per hour, and you shoot a ball out the back at the same speed, it will fall straight down. Now, if you know anything about physics, your first thought upon hearing this might have been the same as mine: “huwhah?” The idea that velocities of equal magnitude and opposite direction cancel each other out in this way is a pretty fundamental result. (Or axiom, depending on how you think about it) It all follows from the Galilean laws of velocity addition: say you have three objects, which I’ll label objects 1, 2, and 3. If the velocity of object 2 relative to object 1 is \(\vec{v}_{12}\), and the velocity of object 3 relative to object 2 is \(\vec{v}_{23}\), the velocity of object 3 relative to object 1 is

In the Mythbusters’ case, object 1 is the road, object 2 is the truck, and object 3 is the ball. If the velocity of the ball with respect to the truck (\(\vec{v}_{23} = -\unit{60}{\mileperhour}\usk\unitx\)) is opposite to the velocity of the truck with respect to the road (\(\vec{v}_{12} = +\unit{60}{\mileperhour}\usk\unitx\)), you get \(\vec{v}_{13} = 0\).

But I don’t really need to go through that argument again — it’s probably been explained thousands of times on other blogs just why this myth seems like it should be painfully obvious. And to be fair, even the painfully obvious stuff needs to be tested sometimes. The idea that any theory or result needs experimental verification to be considered true is even more fundamental than velocity addition. (Heck, even the Galilean laws were eventually shown to be slightly wrong when people started testing special relativity, although that doesn’t change the cancellation of equal and opposite velocities) One might wonder, though, if the physics involved is really so basic, why did it take 3 days for the Mythbusters to get it to work even once?

There is, of course, a straightforward answer to that: it’s really hard to ensure that the speeds of the truck (relative to the ground) and the ball (relative to the truck) match each other exactly. For one thing, speedometers aren’t especially accurate measuring devices. In the US, according to Wikipedia, they’re legally required to display a value between 100% and 105% of the actual speed, but even within those limits, when the speedometer reads \(\unit{60}{\mileperhour}\) your truck could be going as slow as \(\unit{57}{\mileperhour}\). The Mythbusters got around that problem by using a portable tachometer to directly measure the rotation rate of the front wheel. The tachometer is a relatively precise device, and it also measures the rotation of the tire directly rather than trying to infer it from the transmission or something attached to the axle, so it should eliminate most of the uncertainty in the truck’s speed.

However, in order to be able to match the speeds of the truck and the projectile, you have to precisely control both of them, and in the case of the air cannon the Mythbusters were using, that’s not so easy. On the show, they took the smart step of measuring several shots to find out how consistent the cannon actually was, and Grant calculated the standard deviation of their speed measurements to be \(\unit{0.8}{\mileperhour}\). That’s really not bad, especially for a “homemade” air cannon, but it will still have some effect on the experiment and there isn’t any easy way to reduce that deviation further. Whatever variation there is in the cannon’s muzzle velocity will produce some corresponding variation in the ball’s path as it falls. The question is, how much?

That question can be answered by the theory of error propagation. Error propagation tells you how much a small variation in one quantity (like muzzle velocity) affects the value of another, related quantity. In this case, the Mythbusters are looking for the ball to fall straight down as viewed by the high speed camera, and a good way to quantify that is the horizontal displacement of the ball from its launch height down to the ground. The relevant formula is, of course, \(x = v_{13} t\), where \(t\) is the time taken for the fall, given by

Putting it all together we get

where \(h\) is the launch height, \(g\) is the gravitational acceleration, and \(v_{12}\) and \(v_{23}\) are the speeds of the truck with respect to the road and the ball with respect to the truck… respectively. Because the velocity \(\vec{v}_{23}\) is in the \(-\unitx\) direction, I wrote a minus sign in front of it, and that allows me to treat \(v_{23}\) as a positive value.

Remember that what we’re actually trying to do is figure out how much the variation in \(v_{23}\) (the horizontal launch speed of the ball) affects \(x\) (the horizontal distance traveled by the ball on its way down). In this case, it’s going to wind up being pretty simple. The general formula, when you have one dependent variable and one independent variable, is

\(\delta v_{23}\) is the standard deviation (or uncertainty) in muzzle velocity, which we’re taking to be \(\unit{0.84}{\mileperhour}\) for the air cannon, and \(\delta x\) is the resulting standard deviation (or uncertainty) in \(x\). Evaluating the derivative gives

Based on the distances listed in the show and my measurements (literally holding a ruler up to the TV), the height through which the ball falls seems to be almost exactly \(\unit{1.0}{\meter}\). So plugging in numbers gives

That means that if we (actually Kari, Grant, and Tory) measured the horizontal displacement of the ball as it fell, the standard deviation of all those measurements should be about \(\unit{0.38}{\meter}\). But wait, I’m not done yet!

In most cases in physics, we assume that measurements follow what we call a normal distribution — probably given that name because, well, it’s normal for things to be distributed that way. (There are mathematical reasons for that) The normal distribution is a bell-shaped function that tells you, given the average value of some quantity and its standard deviation, just how often you can expect to get a result in any particular range. This is exactly what we have here. Assuming Kari consistently drove the truck at exactly \(\unit{60.}{\mileperhour}\), and assuming that the average muzzle velocity of the air cannon is the average obtained in the test, \(\unit{58.2}{\mileperhour}\), the average horizontal displacement to expect from the ball would be

(It’s pretty close to the standard deviation of \(\unit{0.38}{\meter}\), but that’s just a coincidence.)

Using this average and standard deviation, a plot of the normal distribution looks like this:

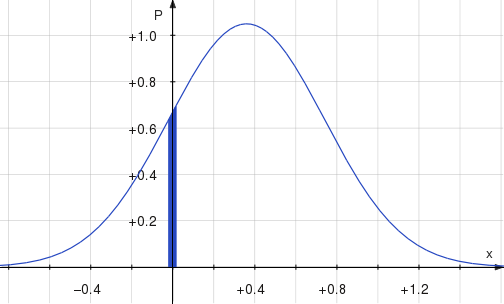
Roughly speaking, this shows, for each possible horizontal distance \(x\), the probability that the ball will move that far to the side as it falls. (Technically it’s a probability density) The shaded region represents the part that’s within \(\unit{1.7}{\centi\meter}\) of zero. That distance, \(\unit{1.7}{\centi\meter}\), is how far my measurements indicate the ball moved horizontally in the trial that Kari, Grant, and Tory considered a success (the last one they put on the show).

If I decide that that’s going to be my criterion for success, namely that the ball moves less than \(\unit{1.7}{\centi\meter}\) horizontally while it falls, then the area of the shaded region represents the probability that any individual trial will be successful. That probability works out to \(0.023\), which means that you’d expect the ball to drop straight down about once in every 44 trials — and that’s after they started using the tachometer. The probability would have been even less before then. No wonder it took so long!