http://scienceblogs.com/dotphysics/2010/06/collisions_kinetic_energy_or_m.php

Took the words right out of my mouth. Or right off my keyboard. Whatever. I’m just happy to see other people are considering the same questions.

But I’ve got a couple of things to add. First of all, kinetic energy can be easily related to momentum using the formula

which tells you directly that an object with the same energy but larger mass will have a larger momentum.

Also, the big question: is it energy or momentum that gives a collision its decapitating power? My thought is that it actually depends on force. Think about this from the point of view of a particle in the neck. This particle doesn’t “know” (as if a particle could “know” anything) how big the sheet of glass hitting it is; it doesn’t “know” how much energy or momentum the glass has. The reason is that energy and momentum are what I’m going to call global properties, basically meaning that the total amount of them possessed by some object comes from contributions from all different pieces of the object. To measure a global property of the glass, you need to have access to the entire piece of glass. But a particle in the neck doesn’t have that access; it only interacts with a few atoms on the edge, so those are the only ones that can influence it. This means that whatever happens to the neck must be determined by local properties, which can be measured at a point, without having access to the entire piece of glass. And the relevant local property is force. (Think about it: when you feel a force from something pushing on you, you can tell how strong the force is without knowing anything about the object exerting it.)

But of course there’s a little more to it than that. The ability to cut through a neck doesn’t just depend on the glass being able to exert enough force; it also requires sufficient force to be maintained across the full diameter of the neck. When the glass first hits the neck, it exerts some force on the neck, which cuts through the first layer of skin, but the neck also exerts the same amount of force on the glass, which slows it down. (Newton’s third law) Since the glass is moving more slowly, it’s going to exert less force on the next layer of skin. The further it goes through the neck, the slower the glass is moving and the less cutting force it exerts. In order to make a clean decapitation, this continual decrease in speed has to leave the glass moving fast enough to cut through a layer of skin after it’s made it all the way through the rest of the neck.

I can even apply some math to this, although there’s not quite enough information to make a precise calculation. Here’s what I do know. The force \(F\) on the glass changes the glass’s momentum according to Newton’s second law, \(F = \ud{p}{t}\) (this is only in one dimension, so I don’t need to make the variables vectors, but I do need to be careful with signs). Momentum is, of course, \(p = mv\), and I can use that and the chain rule to write

So I know how the force affects the glass’s speed. That’s just general Newtonian dynamics. What I don’t know is how the speed affects the force. In other words, how much force does the neck exert on the pane of glass, as a function of their relative speed? If I knew that function, \(F(v)\), I could plug it in to the previous equation and solve the differential equation for \(v\).

To show how that would work, I’m going to make up an example function \(F(v)\), completely out of thin air. Well, not completely out of thin air — I’m going to take the function from… thin air ;-) If you’ve read my previous posts, you may remember the equation for the aerodynamic drag force,

This is precisely the kind of equation we’d want: the force of resistance, as a function of speed, on a solid object moving through some stuff. Specifically, a fluid. Of course, a neck is hardly fluid-like, but this is just an example so it’ll do the job. (You have a better idea?)

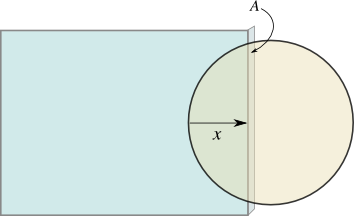
In this situation \(A\) can be the cross-sectional area of the glass that is in contact with the neck, and \(\rho\) will be the volume mass density of neck material (that’s mass per unit volume). But \(\rho\) depends on the full 3D position, so it’s be easier to consider the product of \(\lambda = A\rho\), which is the linear mass density along the direction that the glass moves — in other words, \(\lambda\) is the mass per unit \(x\)-distance that the glass cuts through. It’s a function of only \(x\), not the other coordinates.

If you combine the drag equation with the dynamic equation above it, you get

The negative sign is necessary because the force points in the negative direction. This is a separable differential equation, so we can rearrange it to

and integrate it to get

\(L\) is the total length of the neck that the glass cuts through. (Or you could make \(L\) be some distance partway through the neck, if you wanted to find the glass’s speed there) I started writing \(C\) as \(C(x)\) to remind us that it varies with position, and same with \(\lambda(x)\). Now I can solve for \(v(L)\), the final speed, in terms of \(v(0)\), the known initial speed, and I get

So what does this have to say about the original question? Does a larger piece of glass with the same energy have the same decapitating power?

Well, there’s no reason to expect this formula to be accurate, given all the unjustified assumptions that went into deriving it. But on the other hand, I’d expect that it would have some tenuous relation to reality. If you increase the mass of the neck (say, by making it denser, increasing \(\lambda(x)\)), the equation says the glass loses more speed, which makes sense. And if you increase the mass of the glass, the equation says it retains its speed better, which also makes sense.

Let’s try this out with the Mythbusters’ actual experiment. They tried to simulate the effect of the piece of glass Tory threw, with mass \(\unit{0.45}{\kilo\gram}\), if it were moving at a speed of \(\unit{300}{\mileperhour}\), or \(\unit{134}{\frac{\meter}{\second}}\). According to the calculations they did on the show, that has an energy of \(\unit{4.04}{\kilo\joule}\), and the mass required to reproduce that energy at \(\unit{80}{\mileperhour}\) is \(\unit{6.3}{\kilo\gram}\). So we have two sets of parameters:

The quantity \(\int_0^L C(x)\lambda(x)\udc x\) is going to be the same in both cases. Let me call that \(M\) since it has the units of mass. If I plug in the parameters just listed, I get

Hmm, so this definitely depends on \(M\). Which I don’t know. But if you think about it, \(M\) is basically the mass of neck that the glass cuts through, with some scale factor (related to the “drag coefficient” \(C\)) that’s probably between \(\frac{1}{10}\) and \(10\). (I don’t actually know, I’m just guessing here) A window-thin piece of neck probably has a mass of \(\unit{100}{\gram}\) or less, which means that \(M\) is likely less than \(\unit{1}{\kilo\gram}\). Now look at this plot of \(v(L)\) for various values of \(M\) in that range:

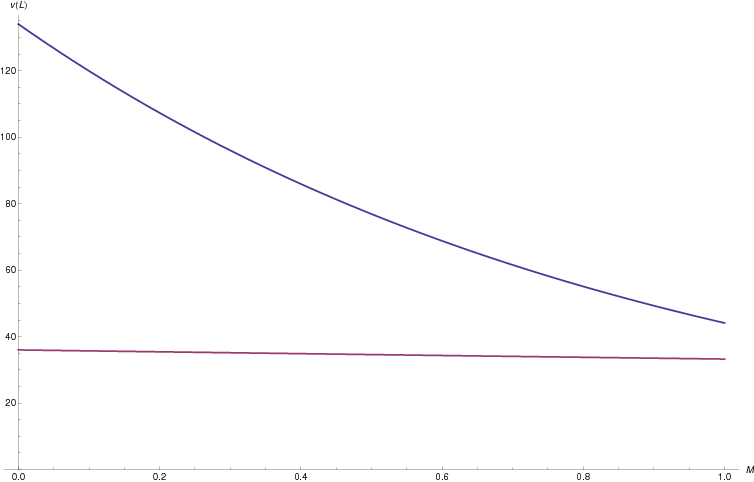
The top curve is for the smaller piece of glass, the one Tory threw, and the bottom line is for the larger piece they put on the truck. Clearly, for this range of values for \(M\), the smaller piece has a much higher final velocity, and that indicates a much higher decapitating power.