Bird Balance

Posted by David Zaslavsky on October 11, 2011 2:50 PM

— Comments

A lot of the discussion about the physics in the latest Mythbusters episode focused on the giant Newton’s cradle. But what about the other myth? While Adam and Jamie were playing around with their giant balls, Kari, Tory and Grant balanced a car on a cliff in order to test whether a bird landing on the hood would be able to send it falling over the edge. Unsurprisingly, it turns out there’s some interesting physics to be found there as well.

Potential Energy and Equilibrium

First of all, what does it take to balance a car on a cliff? The easiest way to think about this physically is in terms of gravitational potential energy. Let’s say that the top of the cliff, at the point where the car is resting on it, is at height zero. Then the potential energy of the car is $U = mgh_\text{cm}$, where $h_\text{cm}$ is the height of the car’s center of mass. As a rough rule of thumb, the car “seeks out” the configuration of lowest potential energy (there are a bunch of caveats to that statement but it’s good enough for now), which means its center of mass is going to fall as low as possible.

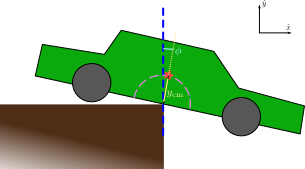Diagram of car teetering on cliff For this car, there are really only two ways it can move: it can rock forward or backward. If the center of mass is behind the edge of the cliff, then rocking forward increases the potential energy, whereas rocking backward decreases it, so the car will tend to tilt backward, keeping it on the cliff. On the other hand, if the center of mass hangs over the edge of the cliff, it’s rocking forward that will decrease the potential energy, so the car will fall off. Mathematically, we can parametrize the position of the center of mass as $\vec{r}_\text{cm} = h_\text{cm}(\unitx\sin\phi + \unity\cos\phi)$ and find the torque acting on the car as

$$\tau = -\pd{U}{\phi} = -\pd{}{\phi}[mgh_\text{cm}\cos\phi] = mgh_\text{cm}\sin\phi$$

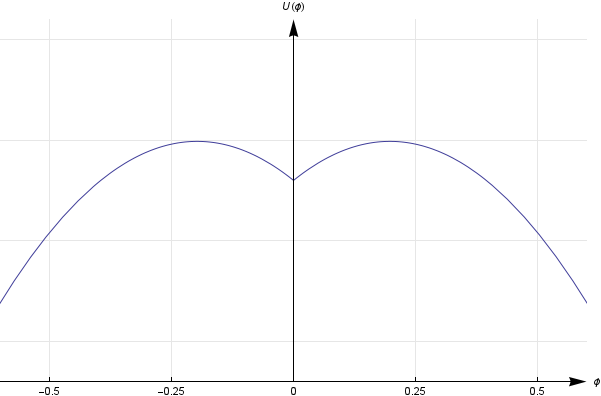
(This is an example of a generalized force, for the curious.) The fact that there is no negative sign in this expression means that we have an unstable equilibrium: the car will be balanced at some particular angle ($\phi = 0$), but as soon as it tips the slightest bit in one direction or the other, the torque is going to push it further and further in that direction. If you look at the graph of potential energy as a function of the angle $\phi$, you’ll see that the balancing point at $\phi = 0$ corresponds to a local maximum of the potential energy, which is the signature of an unstable equilibrium.

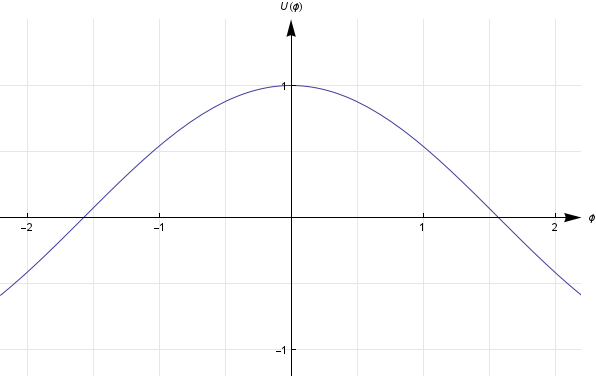
Graph of potential energy as a function of angle for unstable equilibrium

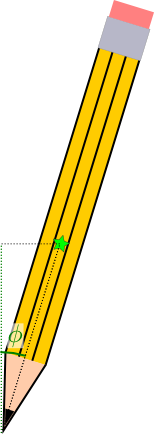Diagram of pencil balancing on tip The thing is, if you have an object in true unstable equilibrium, it’s impossible to actually balance it. Even the tiniest push in one direction or another, like a breeze or a light touch, or even the random thermal motions of the molecules, will be enough to displace the object and get it falling in one direction or another — for an example, try balancing a pencil on its tip. To get an object to actually balance, you need a stable equilibrium, in which pushing the object in one direction or another produces a torque that tends to push it back. This corresponds to a local minimum in the potential energy, as in this graph:

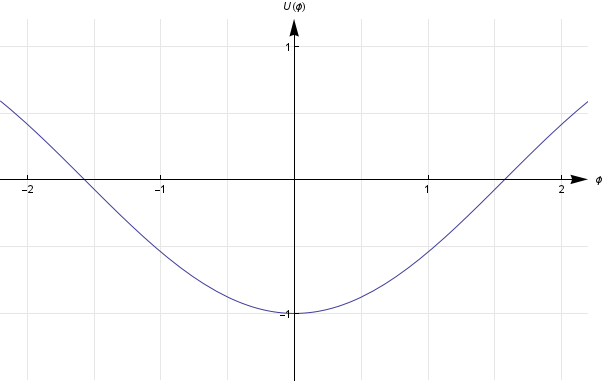
Graph of potential energy as a function of angle for stable equilibrium

Of course, the potential energy for real-world objects usually isn’t just a nice parabola (or cosine curve); in general, it’ll have some combination of maxima and minima. In that case, you can actually have an equilibrium which is stable for small displacements, but unstable for larger displacements. 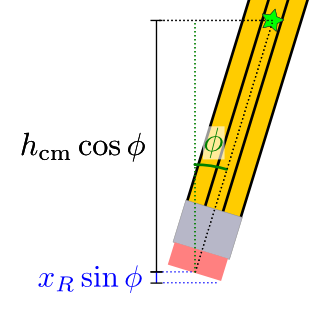Diagram of pencil balancing on eraser For example, consider balancing a pencil on its eraser. (One fresh out of the package, so that the eraser is flat.) If this pencil tips in either direction, its center of mass is going to rise a little bit.

$$U(\phi) = \begin{cases}mg(h_\text{cm}\cos\phi + x_R\sin\phi),&\phi\ge 0 \\ mg(h_\text{cm}\cos\phi - x_L\sin\phi),&\phi\le 0\end{cases}$$

where $x_R$ is the distance along the base of the eraser from the center of mass to the right pivot point (in other words, when the pencil is perfectly upright, $x_R$ is the horizontal distance between the center of mass and the right pivot point), and $x_L$ is the same for the left pivot point. The potential energy graph in that case looks like this:

Graph of potential energy as a function of angle for locally stable equilibrium

This is basically what’s going on with the Mythbusters’ car. Even though being balanced on the edge of a cliff is an unstable situation for large pushes, there’s a little “dip” in the potential energy function which makes it stable for very small displacements. If the car tilts a little bit to the left or right, it will still tend to return to its original position, as long as it doesn’t tilt far enough to escape the dip. This dip could be caused by, say, the bottom of the car getting dented when they were trying to get it into position.

External Forces

Now that we know what it takes to balance a car, let’s figure out what it takes — in physics terms — to knock one over.

When a bird lands on the hood of the car, it has two effects:

It shifts the center of mass of the car-bird system by a small distance toward the bird
Any momentum the bird had when it landed is transferred to the car

Both of these can contribute to moving the car out of its stable equilibrium.

Shifting the Center of Mass

The new center of mass can be computed as a weighted average of the centers of mass of the car and bird individually.

$$\vec{r}_\text{cm} = \frac{m_1\vec{r}_1 + m_2\vec{r}_2}{m_1 + m_2}$$

For this situation, if you treat the horizontal location of the car’s original center of mass as $x = 0$, you can calculate that the new center of mass of the bird-car system shifts by a horizontal distance

$$\Delta x_\text{cm} = \frac{m R}{M + m}$$

where $m$ is the mass of the bird, $M$ that of the car, and $R$ the distance between the bird’s perch and the car’s original center of mass.

Why is this important? If you look at the equation for potential energy a few paragraphs back, you’ll notice that $U(\phi)$ actually depends on the position of the center of mass, through the variables $x_L$ and $x_R$. So when the bird shifts the center of mass, say, to the right, it changes $x_L$ and $x_R$:

$$x_L \to x_L + \Delta x_\text{cm} \qquad x_R \to x_R - \Delta x_\text{cm}$$

which in turn changes the potential energy function:

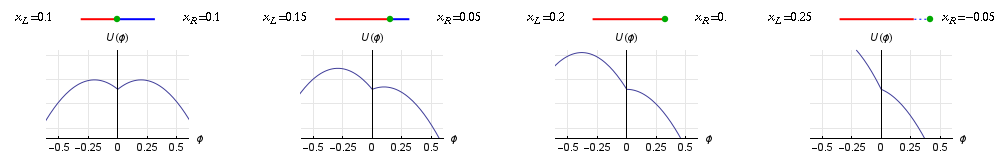
Diagrams showing change in potential energy function with shifting center of mass

As the graphs show, this shift doesn’t change the height of the equilibrium position at $\phi = 0$, at least not at first. But it does reduce the height of the “hump” on the right side, which is going to make it easier for the car to fall. It also moves the position of the hump closer to the current tilt of the car, $\phi = 0$, which means the car doesn’t have to tilt as far before it escapes its stable equilibrium. As an extreme case, if the center of mass shifts all the way over to the right pivot point, we’ll have $x_R = 0$, the hump will disappear, and the car will fall right away. You can confirm this with a calculation of the position of the hump, represented by $\phi_c$ (the “critical” angle at which the car will fall), which lies at the local maximum of the potential energy:

$$\evalat{\ud{U}{\phi}}{\phi_c \ge 0}{} = -mg(h_\text{cm}\sin\phi_c - x_R\cos\phi_c) = 0$$

$$\phi_c = \atan\frac{x_R}{h_\text{cm}}$$

So when $x_R = 0$, the critical angle becomes zero. Since the car is already sitting at $\phi = 0$, it’ll be tilted enough to fall, without any wobbling. That’s what happened at the end of the episode, for example, when Kari filled up the car’s hood with frozen hens.

Momentum Transfer

Even if you don’t shift the center of mass all the way past the pivot point, it’s still possible to make the car tip. As the Mythbusters pointed out in the later part of the episode, the momentum transferred from the bird as it lands might be enough to push the car over the energy “hump,” even if it wouldn’t tip based on the position of the center of mass alone.

To figure out what it takes to make this happen, we need to convert the momentum of the bird to the amount of energy it transfers to the car. The bird’s landing is basically an inelastic collision in which one of the objects rotates around a fixed pivot, and in cases like this, you use conservation of angular momentum. Coming in, let’s say the bird has a landing speed $v$; then its angular momentum around the pivot point will be $L \approx mvR$. Once the bird-car system comes together and acquires this angular momentum, it will have a rotational kinetic energy of

$$K_r = \frac{L^2}{2I}$$

If the bird lands on the very edge of the hood, that’s

$$K_r = \frac{(mvR)^2}{2\beta (m + M) R^2} = \frac{m}{\beta (m + M)}\times\frac{1}{2}mv^2$$

where $\beta$ is the coefficient that appears in the formula for moment of inertia ($I = \beta mr^2$). It depends on the detailed shape of the car, but since a car is roughly the shape of a rod (which has $\beta = \frac{1}{12}$), we can use $\beta \approx 0.1$ as an order-of-magnitude estimate.

When the bird adds this extra energy to the car, it’s not going to stay in place at $\phi = 0$ anymore, because the car-bird system now has more energy than just the potential energy associated with that position. The car is going to tilt downwards, and as it does so it will progressively convert that kinetic energy $K_r$ to more potential energy — remember, its center of gravity is rising as it tilts (at first). If it has enough energy, it will eventually reach the critical angle $\phi_c$, and then the car topples down the cliff; if it doesn’t have enough energy, it will stop at some point before that and start rocking back in the other direction.

Graphically, you can see this by comparing the total energy to the height of the hump:

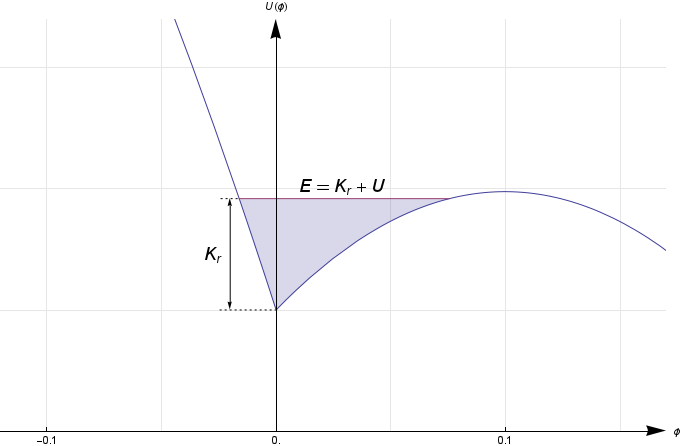
Graph of potential with an example of total energy also plotted

The points at which the total energy line intersects the potential energy line are the points at which the car runs out of energy and rocks back in the other direction — appropriately, they’re called turning points. If the total energy is lower than the hump, the car will oscillate (rock) back and forth between the two turning points. but if the total energy is higher than the hump, there will be no intersection (no turning point) on the right and the car just keeps going in that direction.

Mathematically, the amount of kinetic energy needed to reach the critical angle is

$$K_{r,c} = U(\phi_c) - U(0) = (m + M)g\biggl(h_\text{cm}\cos\atan\frac{x_R}{h_\text{cm}} + x_R\sin\atan\frac{x_R}{h_\text{cm}}\biggr) - (m + M)gh_\text{cm} = (m + M)g\Bigl(\sqrt{x_R^2 + h_\text{cm}^2} - h_\text{cm}\Bigr)$$

Setting this equal to $K_r$ from above shows that the bird needs to land with a speed of at least

$$v = \sqrt{2\beta\biggl(\frac{M}{m} + 1\biggr)^2g\Bigl(\sqrt{x_R^2 + h_\text{cm}^2} - h_\text{cm}\Bigr)}$$

to tip the car.

Estimating Results

OK, so now that all that math is out of the way, let’s plug in some numbers and see whether these formulas make any sense! Remember that there are two different ways for the car to tip: either its center of mass shifts past the pivot point, or it gets enough kinetic energy from the bird to tilt it past the critical angle.

First, let’s check the center of mass shift. In order to calculate that, we need to know the masses of the bird and the car, as well as the distance from the pivot point at which the bird lands. Fortunately, they told us in the episode that the car had a mass of 3000 pounds, so $M \approx \SI{1400}{kg}$, and the heaviest bird they tested was 20 pounds, so $m = \SI{9}{kg}$. The distance between the landing point and the forward pivot point is a little fuzzier, but we do know that it was roughly 6 and a half feet, or $\SI{2}{m}$, from the front of the car to the point where the Mythbusters eventually managed to balance it. In the best-case scenario that the bird lands right on the front of the car, that’s exactly the distance we need. Plugging the values in gives

$$\Delta x_\text{cm} = \SI{13}{mm}$$

Is that enough of a shift to make the car tip? Well, obviously we know from the show that it wasn’t, but in order to calculate an answer, we would have to compare that distance to the size of the dip in the car’s potential energy function — or more precisely, the horizontal distance that the car’s original center of mass would have to move before it passes the cliff-side pivot point. This is something we don’t have any direct information about.

But let’s think about the result another way: in order to allow the car to be tipped by a bird, the Mythbusters would have had to get the center of mass within $\SI{13}{mm}$ of the cliff edge. Does it seem reasonable that they could have managed to do that? I don’t think so. They were having trouble positioning the car any more precisely than to within a few inches, and $\SI{13}{mm}$ is a small fraction of that, so they would have had to have gotten rather lucky to get the positioning exactly right.

What we can do is calculate how close they probably did get it, based on the amount of mass they actually had to put on at the end. Kari dropped 80 frozen hens, each weighing about a pound and a half, plus a mechanical turkey, on the hood of the car, so all we have to do is replace the mass of the bird with the mass of the frozen hens (120 pounds) plus that of the turkey (20 pounds). The total comes out to $\SI{63}{kg}$. Then again, not all the birds were all the way down at the end of the hood, so their “effective mass” would be a bit less than that; I’ll estimate $\SI{55}{kg}$. With this mass, we get almost 6 times as large of a shift:

$$\Delta x_\text{cm} = \SI{77}{mm}$$

This means the Mythbusters managed to find the position of their car’s center of mass to within about 3 inches, less than the width of an average person’s hand. Considering the equipment they had to work with, that’s not bad.

What about the extra kinetic energy from a bird landing on the hood? Conveniently enough, we have a straightforward formula for this one, which tells us how fast the bird would have to have been traveling when it landed. The numbers that go into it are easy enough to estimate: for the moment of inertia coefficient, $\beta \approx 0.1$; we already have $M \approx \SI{1400}{kg}$ and $m = \SI{9}{kg}$ from the show; and gravitational acceleration is of course $g = \SI{9.8}{m s^{-2}}$. The value we just calculated for how precisely they position the car, namely $\SI{77}{mm}$, can go in for $x_R$. The only thing we’re left with is $h_\text{cm}$, the height of the car’s center of mass above its pivot points. We don’t actually know this, but it has to be a little less than half the height of the car, which means $\SI{40}{cm}$ should be a reasonable estimate. Plugging in those numbers, I get

$$v = \SI{18}{m s^{-1}}$$

That’s pretty fast — over 40 miles per hour! Many birds can fly at that speed or faster (including the condor, which goes up to 55 miles an hour), but no bird would actually land on a hard surface going that fast. Given that, it’s clear that the pigeons and hawks and owls never stood a chance. Far from being able to be toppled by a breeze, as Kari speculated during the show, this model suggests that you pretty much would have had to fire a cannonball into the hood for that car to go over the cliff.