Here’s one for the fellow Star Trek fans out there. At the end of Star Trek: Nemesis (SPOILER ALERT), the Enterprise-E and Shinzon’s Romulan warbird, the Scimitar, get involved in a battle in which the Scimitar latches on to the Enterprise using grips. One of the community members at Science Fiction and Fantasy Stack Exchange thought to ask, when the Scimitar fired its engines in reverse, why did it detach from the Enterprise rather than dragging both ships along?

At the question on SFFSE, there are two proposed explanations, the inertia of the Enterprise and the failure point of the grips. Both of them are relevant, but inertia doesn’t explain what happens all by itself. After all, if it were just inertia, what’s to say that the Scimitar detaches from the Enterprise instead of the engines detaching from both ships? As we’ll see, inertia does play a role in determining how much force is exerted on each part of each of the two ships’ structures. But once that force distribution is determined, it really comes down to whether the amount of force on the grips is enough to break them.

In the grand tradition of physics, I’m going to make a simplified model of this situation. Instead of two starships with hulls locked together, consider two boxes connected with massless strings. Suppose you pull on the string on the far right with a force \(F\). What happens to the boxes? Well, Newton’s second law applies to the system of the two boxes as a whole, so the system of both boxes moves to the right with an acceleration \(a = \frac{F}{m_0 + m_1}\).

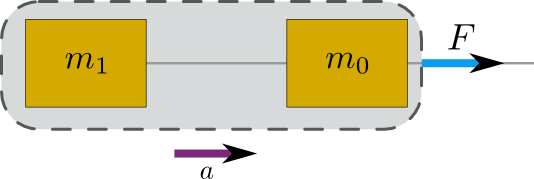
Suppose that the string is stretched out. Both boxes will move together; in other words, each one individually has acceleration \(a\). That means the net force acting on the box on the right is

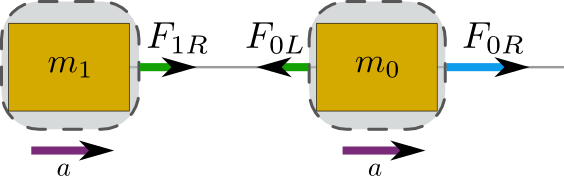
As you can see from the diagram, the box is subject to a rightward force \(F_{0R}\), from the string on the right (that’s just the total pulling force \(F\)), and a leftward force \(F_{0L}\), from the string on the left. Their difference has to be equal to the net force. I can use this equation to determine the value of \(F_{0L}\),

You can apply the same reasoning to the box on the left: it’s subject to a rightward force \(F_{1R}\) and a leftward force of, well, zero. Their difference, which is just \(F_{1R}\), has to be equal to \(m_1 a\):

Notice that the leftward force acting on the box on the right is equal to the rightward force acting on the box on the left. What this means is that the string pulls inward on both ends with the same force. This is just what you’d expect, since if the string is massless, \(F = ma\) with \(m = 0\) tells you that there cannot be any net force acting on it.

Of course, if the string is pulling on the boxes it’s attached to, Newton’s third law says that the boxes must also be pulling on the string, just as hard. So the string itself is experiencing a force of \(\frac{F m_1}{m_0 + m_1}\) stretching it out in both directions. This is the source of the string tension. Now, any object, including a string, will break if it’s subjected to a certain amount of tension. This maximum tension is sometimes called the failure point. In this example, if \(\frac{F m_1}{m_0 + m_1}\) exceeds the failure point of the string, then it will snap.

So how does this apply to the Enterprise and the Romulan warbird? Imagine the warbird as the box on the right, the Enterprise as the box on the left, and the grips that are holding them together as the string. The force \(F\) that pulls to the right now comes from the warbird’s engines.

As with the string connecting the boxes together, the grips that hold the Scimitar to the Enterprise are subject to a tension force of

If this force is greater than the failure point of the grips, they will break. Notice that the inertial mass of the Enterprise, \(m_\text{Enterprise}\), does affect how much force is exerted on the grips.

This case was pretty easy to analyze because it’s obvious that the grips are the weak point in the system of the two ships. But we’d get a better model if we used not just two boxes, but a whole chain of them. The same reasoning used in the case of two boxes applies to a longer chain:

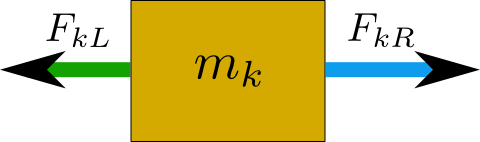1. Let \(m_k\) be the mass of each individual box in the chain, and \(M = \sum_k m_k\) be the chain’s total mass. Then the whole chain moves with acceleration \(a = F/M\).
2. Each block moves with that same acceleration, and so the net force on block \(k\) is \(F_k = m_k a = \frac{F m_k}{M}\).
3. This force arises from a force from the string on the left, \(F_{kL}\), and a force from the string on the right, \(F_{kR}\), whose difference is equal to \(F_k\).
4. Since the strings are massless, \(F_{(k+1)R} = F_{kL}\).
5. Knowing that the rightward force on the rightmost block is zero, you can figure out the tension in each string, starting from the right:

The string on the far right has the most tension, and then the tensions decrease as you move toward the free end of the chain. Each box “absorbs” an amount of force proportional to its mass, reducing the tension by that much for the next string over. That is the effect of inertia.

In this analogy, the boxes represent atoms, and the strings represent the electromagnetic forces that hold atoms together. Using roughly this sort of technique, you could make a “stress map” showing how much force each part of the Enterprise and Scimitar (or any other structure) would be subject to, and use it to predict which parts are most likely to fail. Obviously, it’s more complicated in three dimensions, but this is the basic form of the kind of analysis used by structural engineers and geologists on a daily basis.