There’s been a lot of big news from the experimental physics community over the past week or so, but unfortunately I’ve been busy with spring cleaning and making arrangements for a trip to DIS 2012 so I haven’t been able to keep on top of it. Funny how I have less free time when I’m on vacation…

Anyway, here’s a recap of some of the major recent events in the physics world:

Higgs boson search update

Tevatron combined Higgs signal

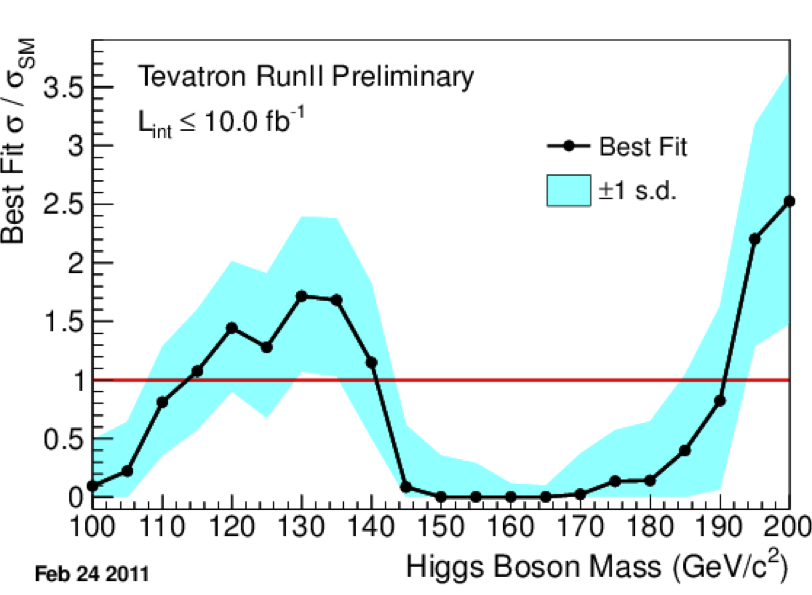At the Moriond conference on electroweak physics, CDF and D0, the two major experiments from the (now closed) Tevatron, reported an excess of collision events between about \(\SI{115}{GeV}\) and \(\SI{140}{GeV}\), peaking at \(2.2\sigma\). This could be a very weak signal of the Higgs boson, but it wouldn’t have been much to get excited about if ATLAS and CMS hadn’t already detected similar (but stronger) signals in the same energy range.

It’s worth keeping in mind that the Tevatron has been shut down, so these latest results aren’t based on new data (like the LHC results); they’re based on a new analysis of the same data that had already been collected as of last year. The main reason they were able to discover this excess where they hadn’t seen it before was an improved technique for b-jet tagging; that is, identifying processes where the Higgs boson (perhaps) decays into a bottom quark and anti-bottom quark.

ATLAS Higgs exclusion and signal suppression

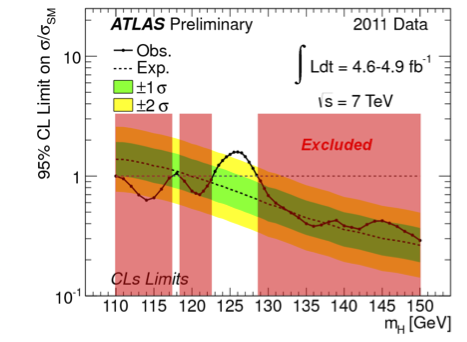Speaking of the LHC expreiments, at the same conference the ATLAS collaboration presented their latest results, in which they have found… well, mostly nothing. But in part, this is a good nothing. What I mean is that the cross sections observed by ATLAS are \(2\sigma\) below what would be expected from the standard model Higgs boson at most energies other than this little window around \(\SI{125.0}{GeV}\). So we’re basically 95% sure that there is no Higgs boson with a mass less than \(\SI{122.5}{GeV}\) or greater than \(\SI{127.5}{GeV}\). This is actually half the battle in finding the Higgs boson directly: we have to not only show that it does show up at a particular energy (which corresponds to its mass), but that it doesn’t show up at other energies.

On the other hand, in this energy range around \(\SI{125.0}{GeV}\) where we suspect that the standard model Higgs is showing up, the latest ATLAS data have actually decreased the significance of the peak. You may remember that back in December, ATLAS and CMS announced that they were seeing a pretty tall peak around \(\SI{126}{GeV}\), which they took as a possible first indication of the Higgs boson. The hope was that if that really is the standard model Higgs, as more data came in the peak would get taller, which would mean that we could be more confident that it’s not a fluke. But the opposite actually happened; when you take the new data into account, the peak is smaller than it was before. It’s still enough to qualify as a region of interest, though, so the overall situation is much the same: there might be a Higgs boson at \(\SI{125}{GeV}\) or so, we’re just not sure yet.

CMS diphoton Higgs signal enhancement

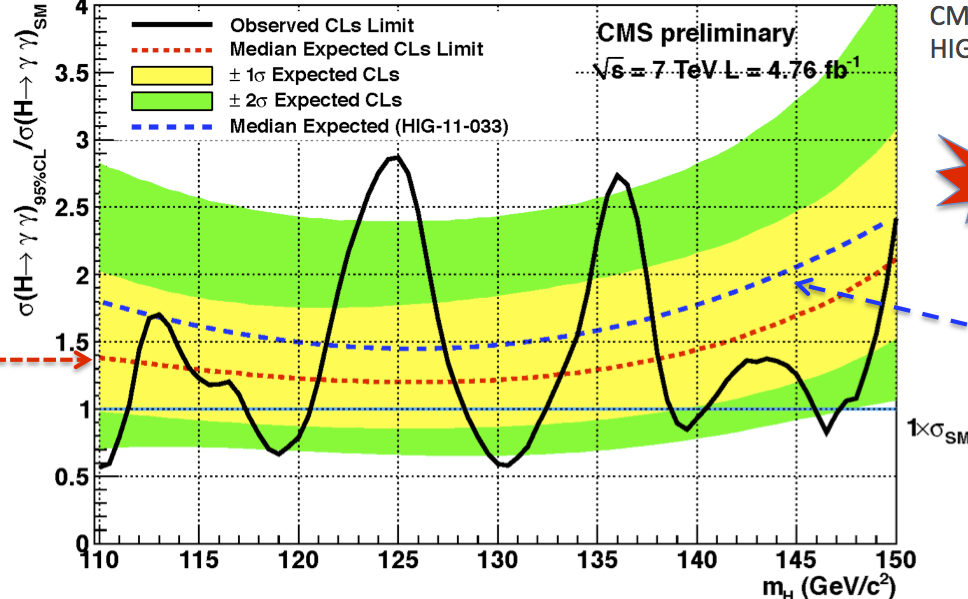CMS, on the other hand, didn’t have much to add to their presentation from December. The main improvement they did make was a better analysis of the events in which they detected two photons that might have come from a decaying Higgs boson. In contrast to the ATLAS results, this new analysis increased the height of the peak, which means CMS is a little more confident that they are seeing something real.

The Last Neutrino Mixing Angle

In other news, the Daya Bay neutrino experiment has announced a measurement of the neutrino mixing angle \(\theta_{13}\). This one deserves a bit more explanation, but I’ll still have to be brief for now. (I am happy to do a more detailed and/or less technical explanation of this if people would like to see it — leave requests in the comments.)

If you’ve studied neutrino physics in any detail, you know that neutrinos have flavor eigenstates and mass eigenstates, but the two are not exactly the same. What this means is that if you produce or detect a particular type of neutrino, such as an electron neutrino, it is actually in a quantum superposition of different masses, and if you are dealing with a neutrino with a particular type of mass, it is in a quantum superposition of different flavor states. This is how neutrinos are able to oscillate: they are created in a particular flavor state, for example \(\ket{\enu}\), travel through space as a superposition of mass eigenstates \(U_{e1}\ket{\mathrm{\nu}_1} + U_{e2}\mathrm{\nu}_2 + U_{e3}\mathrm{\nu}_3\) (“rotating” through different flavor states in the process), and then are detected in some flavor state which may differ from the initial one. The matrix \(U\) which relates the two bases to each other is called the neutrino mixing matrix, or the PMNS matrix, and it can be written as a product of three 2D rotation matrices (sort of):

I’m using Wikipedia’s abbreviations of \(c_{ij} = \cos\theta_{ij}\) and \(s_{ij} = \sin\theta_{ij}\). The \(\theta_{ij}\)s are the mixing angles which quantify the overlap between the flavor states and the mass states.

Starting in the 1960’s, we’ve been able to determine values for two of the angles: \(\theta_{12}\approx\SI{34}{\degree}\) from measuring how neutrinos produced in the sun oscillate on the way to Earth, and \(\theta_{23}\approx\SI{45}{\degree}\) from the oscillations of neutrinos produced by cosmic rays striking the atmosphere. But \(\theta_{13}\) proved to be a lot trickier because there wasn’t a natural physical situation that allowed for a precise measurement of that one angle without involving the other two. The best that previous experiments were able to determine was that the angle is very small. It could have even been zero, which would be unfortunate because that would completely ruin our best chance at measuring the phase \(\delta\). That phase controls CP violation in neutrinos, which in turn is related to the origins of matter in the universe, so… you might say it’s kind of an important number.

Recently, there have been three experiments (that I know of) trying specifically to measure \(\theta_{13}\): T2K, Double Chooz, and Daya Bay. It turned out that Daya Bay was the first to come up with a definitive nonzero value of around \(\SI{5}{\degree}\). The measurement comes at a significance of \(5.2\sigma\), which means they can say \(\theta_{13}\neq 0\) with less than a one in a million chance of being wrong.

Antihydrogen Spectroscopy

In other news, the ALPHA experiment at CERN (not affiliated with the LHC) has measured the spectral lines of an antihydrogen atom for the first time. Their measurement isn’t yet precise enough to compare with the spectral lines of hydrogen to see if they match, but it is a key first step. Comparing the spectral lines is one of the best ways we have to establish whether the electromagnetic force works the same way on antimatter as it does on matter, and that in turn could shed light on possible violations of CP symmetry.

The 230% Efficient LED

Physicists at MIT have developed a light-emitting diode that operates at an efficiency of 230%: it outputs more than twice as much energy as light as the electricity it takes in! That sounds rather crazy at first, but it actually works without breaking any physical laws, because what it really does is convert vibrational thermal energy into thermal radiation. In this sense it kind of acts like a refrigerator, in that it uses a certain amount of input energy to transfer a larger amount of energy from one thermal reservoir to another. Usually the output of a refrigerator is considered wasted energy, like when it gets vented off the coils at the back of your kitchen fridge, but the MIT group has basically found a way to make that “waste” heat actually useful: just let it be emitted as light.

Information and Thermodynamic Entropy

Another group collaborating between multiple institutions has experimentally demonstrated for the first time that the loss of information in any physical system produces heat. This effect was quantitatively predicted by Rolf Landauer in 1961. It’s actually fairly simple to understand: the minimum number of physical states of a system that stores \(N\) bits of information is \(2^N\), and the entropy of a system with that many states is \(S = Nk\ln 2\). So if a system goes from storing, say, one bit to none, it has to lose an amount of entropy equal to \(k\ln 2\). But in order for the second law of thermodynamics to be satisfied, something in the system’s environment has to increase its entropy by at least that much, and doing so requires a heat transfer of \(\Delta Q = T\Delta S = kT\ln 2\).

Despite the simplicity of the theoretical argument, nobody had managed to experimentally observe this effect until now, because the amount of heat being exchanged is tiny, around \(\SI{e-21}{J}\) at room temperature. Besides, the way that most common systems store information is highly redundant, so when you lose one bit of the information you thought you were storing, you might actually be losing many bits of physical information. This is intentional, of course, because you don’t want a random thermal fluctuation wiping out half your hard drive! But it tends to get in the way of physics. So the team which performed this experiment had to construct a device which actually stores one and only bit of information, using an optical trap between glass panes, and measure its energy changes very precisely. When they did so, they found amounts of heat being dissipated that satisfied the Landauer bound very cleanly.

Upcoming events

The Moriond conference continues this coming week, with its focus shifting to QCD, so perhaps there will be more exciting news from the LHC or Tevatron experiments, or who knows what else. I’ll definitely be watching to see what comes out of it, and I’ll be posting any interesting results from Moriond or elsewhere to my Twitter stream, so keep an eye on that to stay informed! Otherwise, perhaps I’ll have to write another summary blog post if it turns out to be another big week.

P.S. I should acknowledge that I grabbed the images in this article from Résonaances, just because I’m lazy (the original source is, of course, the relevant conference presentation).