Careful, the rope is out to get you!

Posted by David Zaslavsky on May 16, 2013 5:28 PM

— Comments

I know, I know, this blog post is very late! If I’m going to post about a Mythbusters episode, I usually try to do it before the next one airs. But this topic — calculating the circumstances under which a rope will pull a person’s leg — turned out to be pretty complicated. Which of course made it impossible to give up on.

And after days of toil, I think I finally figured it out! If you’re the kind of person who finds complicated physical interactions fascinating, you’re going to love this post. The math isn’t too complicated; if you know what a differential equation is, you’ll be fine, but the physical reasoning is something you could probably spend a while wrapping your head around.

The setup

On the Deadliest Catch-themed Mythbusters episode which came out last week, one of the myths being tested was that if a person steps in a coil of rope, and that rope is attached to a crab pot (trap) that gets dropped over the side of the ship, the rope will be pulled tight enough around the person’s leg that it will drag them overboard, and down to the ocean floor, along with the trap. Now, whether this works can depend on how the rope is coiled, which direction it’s pulled, whether it gets knotted, and so on, but at its core, the myth is about friction. The frictional force between the rope and the leg has to be high enough to keep the rope from slipping while it pulls the person overboard. And friction doesn’t need knots. I’ve managed to develop a model for how friction affects the behavior of a rope coiled around a cylindrical object.

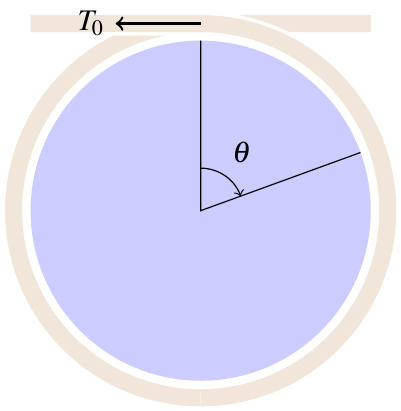
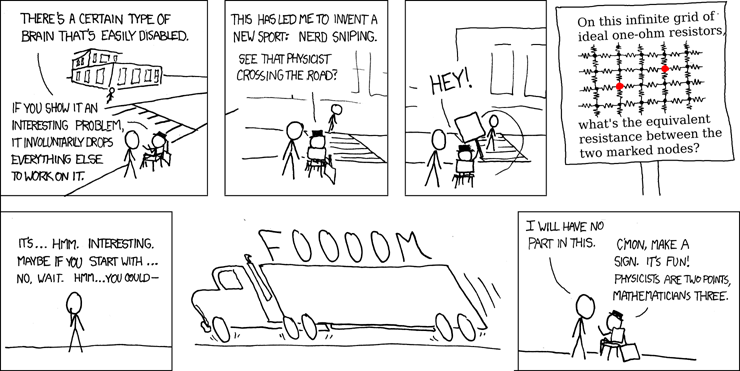
Here’s how it works: Imagine a very short, infintesimally short, segment of the rope. It’s subject to four forces: tension $T_L$ pulling to the left, tension $T_R$ pulling to the right, the normal force $F_N$, and the frictional force $F_f$ which opposes the motion of the rope.

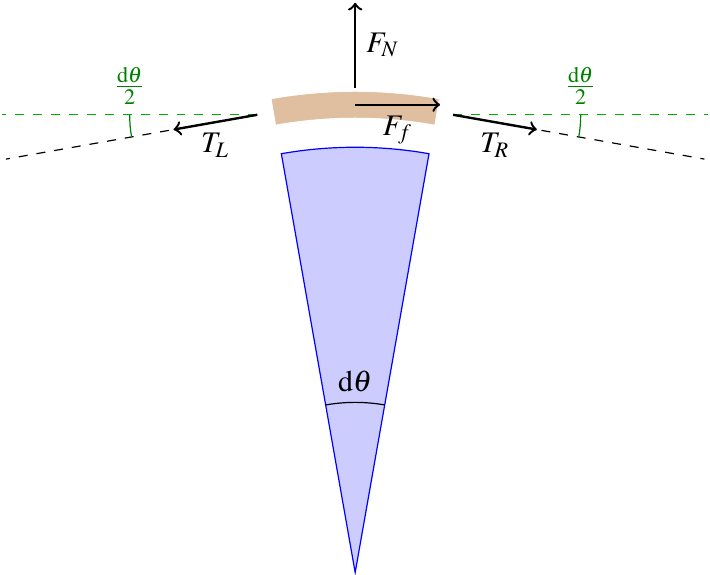
Diagram of infinitesimal segment of rope

Let’s decompose these forces in cylindrical coordinates, using the unit vectors $\unitr$ and $\unittheta$, parallel and perpendicular to the rope respectively. The normal force and friction will be in the radial and tangential directions, respectively, but the tension at each end points slightly off-axis. I’ve marked out the angles in the diagram to show how to decompose the tensions:

$$\begin{align}\vec{T}_L &= T_L\biggl(-\unitr\sin\frac{\udc\theta}{2} - \unittheta\cos\frac{\udc\theta}{2}\biggr) = T_L\biggl(-\unitr\frac{\udc\theta}{2} - \unittheta\biggr) \\ \vec{T}_R &= T_R\biggl(-\unitr\sin\frac{\udc\theta}{2} + \unittheta\cos\frac{\udc\theta}{2}\biggr) = T_R\biggl(-\unitr\frac{\udc\theta}{2} + \unittheta\biggr)\end{align}$$

Time to move on to Newton’s second law. Here’s the radial component of $\sum\vec{F} = m\vec{a}$:

$$\unitr\cdot\sum\vec{F} = -T_L\frac{\udc\theta}{2} - T_R\frac{\udc\theta}{2} + F_N = m\unitr\cdot\vec{a}$$

and the tangential component:

$$\unittheta\cdot\sum\vec{F} = -T_L + T_R + F_f = m\unittheta\cdot\vec{a}$$

From here, there are two cases to consider. If the rope slips, we have $F_f = \mu_k F_N$, and if not, we have an inequality, $F_f \le \mu_s F_N$.

Slipping rope

For simplicity, let’s take the equality first, in which we assume that the rope is slipping. We can put all these equations together by solving for $F_N$ and $F_f$ and using substitution. That gives

$$T_L - T_R + m a_\theta = \mu_k\biggl((T_L + T_R)\frac{\udc\theta}{2} + m a_r\biggr)$$

Since $T_L$ and $T_R$ are the tensions at infinitesimally close positions, their difference will be an infinitesimal quantity, $T_R - T_L = \udc T$. Also, the mass of the segment of rope will be an infinitesimal $\udc m$, which is equal to $R\lambda\udc\theta$ where $R$ is the radius of the coil and $\lambda$ is the rope’s mass per unit length. Putting all this in, we get

$$-\udc T + a_\theta R\lambda\udc\theta = \mu_k T\udc\theta + \mu_k a_r R\lambda\udc\theta$$

I’ve set $T_L + T_R = 2T + \udc T$ and then ignored the second-order term proportional to $\udc T\udc\theta$. This leads to the differential equation

$$\ud{T}{\theta} = R\lambda(a_\theta - \mu_k a_r) - \mu_k T$$

which is the final formulation of the model. It’s a general model, which can apply to several different situations; to get a specific solution, we just need to characterize the rope’s acceleration by postulating some form for the components of the acceleration, $a_\theta$ and $a_r$.

Example solution: the fixed cylinder

To get a feel for this model, I’m going to investigate a simple situation where the cylinder stays in place and the rope slips around it. The rope’s acceleration will be in the tangential direction, $\vec{a} = -a\unittheta$, setting $a_\theta = -a$ and $a_r = 0$.

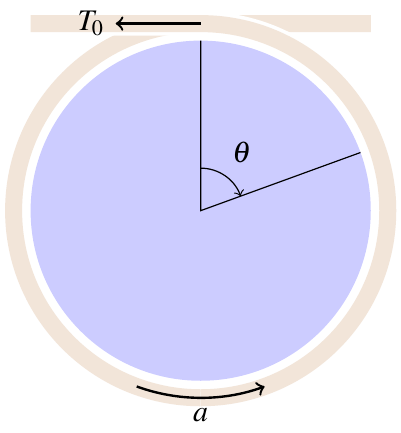
Diagram of rope slipping around a stationary cylinder

With these conditions, the solution to the differential equation is

$$T = -\frac{R\lambda a}{\mu_k} + \biggl(T_0 + \frac{R\lambda a}{\mu_k}\biggr)e^{-\mu_k\Delta\theta}$$

where $\Delta\theta$ is the total angle by which the rope is wrapped around the leg — $2\pi$ for each complete loop. This solution has the form

$$T = T_\infty + (T_0 - T_\infty)e^{-\mu_k\Delta\theta}$$

where $T_0$ is the tension at $\theta = 0$ — where the rope just starts wrapping around the cylinder — and $T_\infty = -\frac{R\lambda a}{\mu_k}$ is a constant, the asymptotic value of the tension after it’s wound around the cylinder many times. Here’s a sample plot:

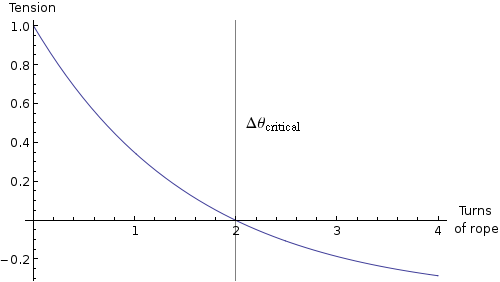
Plot of tension versus turns of rope for a slipping rope

Wait a minute — a negative asymptotic value? Does it even make sense for tension to be negative? Of course not, and here’s where a bit of physical intuition comes into play. We know our function $T(\Delta\theta)$ starts out positive, $T(0) > 0$, and, if the rope is wound enough times, it ends up negative, $T(\infty) < 0$. That means that for some intermediate angle, the function hits zero. Physically, that’s the point at which the friction between the cylinder and the rope has “accumulated” enough to cancel out the external force applied to the rope. Any further along than that critical angle, the rope is slack, and the function $T(\theta)$ ceases to be applicable.

But wait! We can actually solve for the critical angle at which the tension hits zero.

$$\Delta\theta_\text{critical} = \frac{1}{\mu_k}\ln\frac{T_\infty - T_0}{T_\infty} = \frac{1}{\mu_k}\ln\biggl(1 + \frac{T_0\mu_k}{R\lambda a}\biggr)$$

Let’s do a few sanity checks on this formula:

Greater initial tension $T_0$ corresponds to a greater critical angle. Which makes sense because the harder you pull, the more of the rope you’ll be able to pull taut.
The critical angle decreases as $\mu$ gets larger — which, again, makes sense, because with a rougher pole, your pull won’t be felt as far along the rope.
In the opposite limit, as $\mu$ goes to zero (a frictionless pole), the critical angle becomes $\frac{T_0}{R\lambda a}$. Now, if you take this criterion $\Delta\theta = \frac{T_0}{R\lambda a}$ and rearrange it, you get $T_0 = (R\lambda\Delta\theta)a$, which is just $\sum F = ma$ for a rope on a frictionless surface! As it should be. If this complicated model that handles friction gave the wrong answer when there is no friction, it wouldn’t be much good at all!

That last item in particular also suggests a physical interpretation of this formula: it’s effectively an equation of motion, filling the same role as $\sum F = ma$. Whereas we’d ordinarily use Newton’s second law to calculate the motion of a rope subject to a given force, for the rope sliding around a pole (or leg) we can use this formula instead, and it will take care of the friction and the changing tension over the length of the rope. This works because at the end of the rope, where it “stops” winding around the cylinder, its tension is zero — it’s not pulling anything. (Except perhaps some additional length of rope, but I’m going to assume that’s negligible for simplicity.)

Non-slipping rope

The analysis if the rope doesn’t slip is nearly the same, except that the coefficient of friction is $\mu_s$ instead of $\mu_k$, and instead of an equation, we get an inequality from $F_f \le \mu_s F_N$.

$$T_L - T_R + m a_\theta \le \mu_k\biggl((T_L + T_R)\frac{\udc\theta}{2} + m a_r\biggr)$$

Following the same procedure from before, this becomes

$$\ud{T}{\theta} \ge R\lambda(a_\theta - \mu_s a_r) - \mu_s T$$

OK, this is new. Everybody (well, everybody who has a geeky streak) knows about differential equations, but when have you ever seen a differential inequality? They’re not that common. But it’s not really that hard to understand. In order for the inequality to be satisfied, the rate at which tension changes as you move along the rope (as in the previous section, $\ud{T}{\theta}$ is negative) has to be greater than the particular combination of acceleration and tension that appears on the right. Physically, the left side is related to the strength of friction, the right side is related to the other forces acting on one segment of rope, and for the rope not to slip, friction has to be strong enough to cancel out the other forces at every point along the contact surface.

Example solution: the moving cylinder

It’ll be easiest to make sense of this differential inequality by choosing a specific type of acceleration, as we did with the slipping rope. Let’s say the rope just pulls the cylinder in the direction of the initial tension, namely the $-\unitx$ direction, without rotating it.

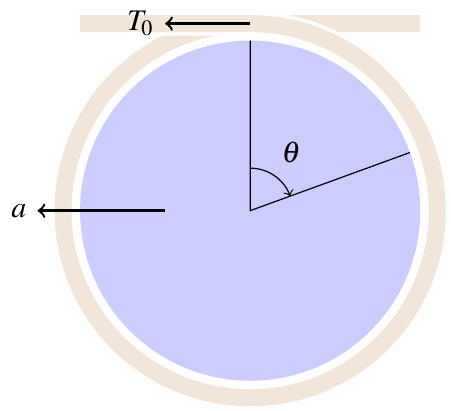
Diagram of rope pulling cylinder in one direction

This is not really realistic, since there will actually be some torque on the cylinder that will also rotate it, but it’s close enough for demonstration purposes.

The components of acceleration in this case will be $a_r = \unitr\cdot\vec{a} = -a\sin\theta$, and $a_\theta = \unittheta\cdot\vec{a} = -a\cos\theta$.

Substituting these in, we get

$$\ud{T}{\theta} \ge R\lambda(\mu_s a \sin\theta - a\cos\theta) - \mu_s T$$

There’s still the little problem that this is an inequality, not an equation. But I have a plan. First, let’s solve the corresponding differential equation; it gives

$$T = \frac{R\lambda a}{1 + \mu_s^2}\biggl((\mu_s^2 - 1)\sin\Delta\theta - 2\mu_s\cos\Delta\theta\biggr) + \biggl(T_0 + \frac{2R\lambda a\mu_s}{1 + \mu_s^2}\biggr)e^{-\mu_s\Delta\theta}$$

or equivalently

$$T = T_\infty\biggl(\cos\Delta\theta - \frac{\mu_s^2 - 1}{2\mu_s}\sin\Delta\theta\biggr) + \biggl(T_0 - T_\infty\biggr)e^{-\mu_s\Delta\theta}$$

with $T_\infty = -\frac{2R\lambda a\mu_s}{1 + \mu_s^2}$. This function gives a value of tension that, if we plug it back into the differential equation, represents the minimum possible rate at which tension can change over the length of the rope.

Now, given that the starting value is fixed at $T_0$, there’s no way the actual tension can dip below the value specified by this function without the rate of change $\ud{T}{\theta}$ being less than the minimum specified by the differential equation. This follows from the mean value theorem. Evidently the tension in the rope can be no less than the function we found from the differential equation; that is,

$$T \ge T_\infty\biggl(\cos\Delta\theta - \frac{\mu_s^2 - 1}{2\mu_s}\sin\Delta\theta\biggr) + \biggl(T_0 - T_\infty\biggr)e^{-\mu_s\Delta\theta}$$

This is the condition that must be satisfied for the rope not to slip. It corresponds to the shaded region in this plot:

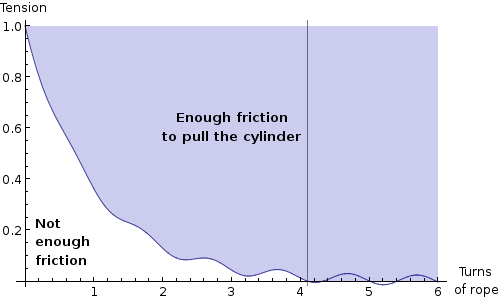
Plot of tension versus turns of rope for a non-slipping rope

Now that that’s cleared up, let’s look at the properties of this solution. Again, the asymptotic value (actually, an asymptotic amplitude of sorts) is negative, which means this function crosses zero somewhere. But now there are those pesky sine and cosine factors, and unfortunately they make it impossible to find a symbolic formula for the critical angle where the tension drops to zero. We can still calculate $\Delta\theta_\text{critical}$ numerically, we’ll just need actual values for all the constants involved. As in the last section, the equation for the critical angle where $T = 0$ defines some relationship between $a$, $\mu_s$, $R$, $\lambda$, $\Delta\theta$, and $T_0$, which we can use as a “smart” stand-in for $\sum F = ma$.

Will the cylinder move?

Now the key question is, if you have a rope wrapped around a cylinder (like someone’s leg) and you pull it, will the rope pull the person, or will it slip? It all comes down to whether the force of friction is strong enough to resist the other forces applied to the rope. Mathematically, that corresponds to whether the differential inequality in the last section is satisfied (at least up to the critical angle where the tension goes to zero). If the inequality is violated at any point along the rope, it’ll slip, but otherwise the rope stays pressed against the cylinder and pulls it.

To figure out whether that happens, we’ll need values of $a$, $\mu_s$, $R$, $\lambda$, $\Delta\theta$, and $T_0$. We plug them into the formula, then set $T = 0$ on the left side (which should be true at the end of the rope, in this simplified model) and see whether the inequality is satisfied. If if is, that puts us in the shaded region of the graph, where friction is strong enough to keep the rope from slipping. Otherwise, we’re in the unshaded region where friction is just not strong enough and the rope slips.

There’s just one problem: what’s the acceleration? The values of $\mu_s$, $R$, and $\lambda$ are readily available (they would be measured), and the experimenter can control the initial tension $T_0$, but we don’t know $a$. Or do we? Well, look at this from an outside perspective. The initial tension exerted on the rope, $T_0$, has to pull the rope itself and the person. If you look at the rope and person as one physical system, a “black box” if you will,

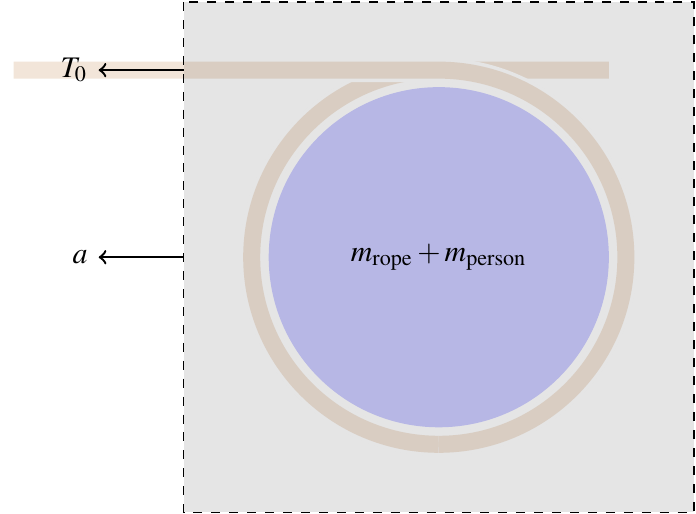
Diagram of rope and cylinder as black box

you can ignore the effect of friction and just use Newton’s second law, $T_0 = (m_\text{person} + m_\text{rope})a$.

$$a = \frac{T_0}{m_\text{person} + m_\text{rope}}$$

which gives us

$$T_\infty = -\frac{2R\lambda\mu_s T_0}{(1 + \mu^2)(m_\text{person} + m_\text{rope})}$$

Numbers: do they work?

Even though this model is unrealistic, chiefly because it doesn’t take into account the rotation of the cylinder due to the tension being off-axis, I still want to try plugging some numbers in. Here are my estimates:

Radius of the leg: $R = \SI{6}{cm}$
Density of the rope: $\lambda = \SI{50}{g/m}$
Static friction coefficient: $\mu_s = 0.2$ (maybe a little low)
Total mass of the rope: $m_\text{rope} = \SI{1}{kg}$
Total mass of the person: $m_\text{person} = \SI{80}{kg}$
External force exerted on the rope: $T_0 = \SI{800}{lbf.} \approx \SI{3500}{N}$, I figure it’s roughly the weight of the crab pot, which was stated to be 800 pounds in the show — though if you ask me, they did not look that heavy. (It turns out not to matter anyway.)

Now yes, I could have used these values for the graph in the earlier section, but I didn’t want to give the answer away! Here’s what the plot actually looks like:

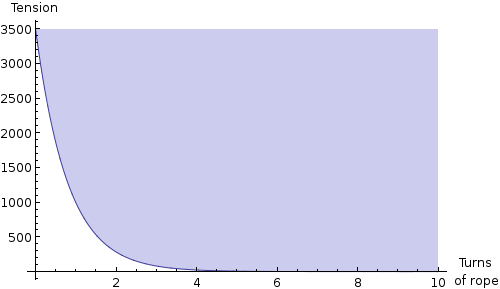
It’s hard to tell there, so let’s have a closer look:

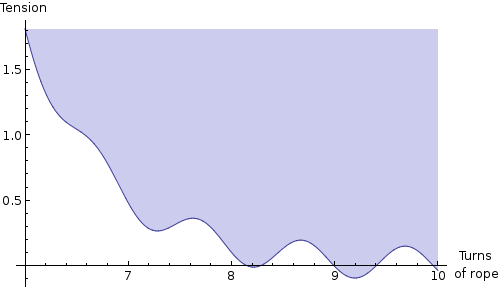
Zoomed plot of tension versus turns of rope

The tension hits zero for the first time just past 8, which means that with these numbers, it takes about 8 turns of rope around your leg to pull you. Any less, and the rope will just slip off.

That’s kind of a lot. But what if we up the coefficient of friction? $\mu = 0.4$ is still probably reasonable, maybe even low, for a rope (they’re made somewhat rough, after all, so that they don’t slip through your fingers). Doubling the friction coefficient gives this plot (already zoomed in):

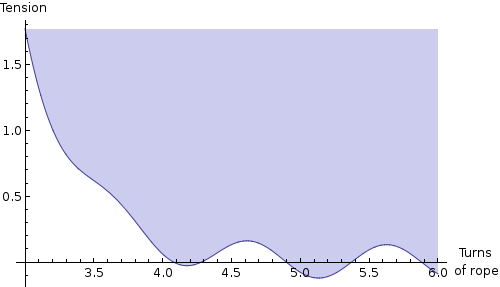
Zoomed plot of tension versus turns of rope for higher friction

Now it only takes four turns for the rope to grab you. I wouldn’t form a conclusion on this myth based on the math alone, but compared to what Adam and Jamie found, it seems not too far off from reality!