It’s that time again: Mythbusters is back! And they sure know how to kick things off with a bang — or better yet, a prolonged burn!

For the 10th anniversary of the show, the Mythbusters revisited the very first myth they ever tested, the JATO rocket car. Wikipedia has the story in what appears to be its most common form:

The Arizona Highway Patrol came upon a pile of smoldering metal embedded into the side of a cliff rising above the road at the apex of a curve. the wreckage resembled the site of an airplane crash, but it was a car. The type of car was unidentifiable at the scene. The lab finally figured out what it was and what had happened.

It seems that a guy had somehow gotten hold of a JATO unit (Jet Assisted Take Off - actually a solid fuel rocket) that is used to give heavy military transport planes an extra ‘push’ for taking off from short airfields. He had driven his Chevy Impala out into the desert and found a long, straight stretch of road. Then he attached the JATO unit to his car, jumped in, got up some speed and fired off the JATO!

The facts, as best could be determined, are that the operator of the 1967 Impala hit JATO ignition at a distance of approximately 3.0 miles from the crash site. This was established by the prominent scorched and melted asphalt at that location. The JATO, if operating properly, would have reached maximum thrust within five seconds, causing the Chevy to reach speeds well in excess of 350 MPH, continuing at full power for an additional 20-25 seconds. The driver, soon to be pilot, most likely would have experienced G-forces usually reserved for dog-fighting F-14 jocks under full afterburners, basically causing him to become insignificant for the remainder of the event. However, the automobile remained on the straight highway for about 2.5 miles (15-20 seconds) before the driver applied and completely melted the brakes, blowing the tires and leaving thick rubber marks on the road surface, then becoming airborne for an additional 1.4 miles and impacting the cliff face at a height of 125 feet, leaving a blackened crater 3 feet deep in the rock.

Most of the driver’s remains were not recoverable; however, small fragments of bone, teeth and hair were extracted from the crater, and fingernail and bone shards were removed from a piece of debris believed to be a portion of the steering wheel.

It’s a fascinating story and all, but there’s plenty of evidence to suggest that this didn’t happen, and in fact that it can’t happen as described. Not only does the Arizona Highway Patrol have no record of ever investigating a case like this, but it’s been tested no less than three times on Mythbusters.

• The first time, on the pilot episode in 2003, Adam and Jamie found that a Chevy Impala with three hobby rockets on top, providing equivalent thrust to a JATO unit, wouldn’t get anywhere close to \(\SI{350}{mph}\), though it did exceed the \(\SI{130}{mph}\) top speed of the chase helicopter.
• The second time, in 2007, they found that… rockets explode sometimes. Hey, it’s Mythbusters, you can expect nothing less. :-P
• The third time was the 10th anniversary special that aired last week. With more power than the equivalent of one JATO unit, the car still didn’t get much faster than about \(\SI{200}{mph}\). In this iteration, the Mythbusters also tested the part of the myth in which the car supposedly took off and flew through the air — which also failed spectacularly (in every sense of the word), with their test car running off a ramp and nosediving into the desert.

There’s a lot of juicy physics in this myth. But it breaks down into a couple of key parts: first, can a rocket-powered Impala even make it up to \(\SI{350}{mph}\)? And secondly, if it did, could it fly a mile and a half through the air? I’m going to handle the speed issue here, and get into the fable of the flying car for a later post.

Before it becomes airborne, a JATO car is just an object subject to three forces: the thrust of the rocket and the engine force pointing forward, and air resistance pointing backward. Well, there’s also tire friction, but that’s a lesser influence. In the simplified model I’m going to use, three of these forces are constant — the thrust and engine force forward, and tire friction backward — and air resistance is the one velocity-dependent force. For convenience I’ll group all the constant forces under the name drive force, \(F_\text{drive}\).

With the forces as described, a car is pretty similar to a falling object, which is also subject to a constant force in one direction and air resistance in the other. Like, say, an airplane pilot who fell out of his plane at \(\SI{22000}{ft.}\), which I’ve already worked through the math for in an earlier blog post. Here’s how that same math applies to the JATO car: first write Newton’s second law \(\sum F = ma\), including the drive force \(F_\text{drive}\) and the air resistance \(F_\text{drag}\),

The car’s terminal speed is the speed at which its acceleration, \(\ud{v}{t}\), is zero. Plugging that in, we get

Now we can rewrite Newton’s second law like so:

This makes it easy to see that if an object is moving faster than its terminal speed at any point, that is \(v > v_T\), it will tend to slow down (because \(\ud{v}{t} < 0\)), and if it’s moving slower than its terminal speed, \(v > v_T\), it will speed up. It’ll only stay at a steady speed if \(\ud{v}{t}\approx 0\), and that requires \(v \approx v_T\), i.e. that the object is traveling roughly at its terminal speed.

The story from Wikipedia has the car barreling down the road at more than \(\SI{350}{mph}\) for several seconds, which suggests that for a JATO Impala, \(v_T \gtrsim \SI{350}{mph}\). Is that realistic? Well, we do have some of the information necessary to figure it out. As reported in the Mythbusters pilot, the thrust of a JATO is about \(\SI{1000}{lbf.}\), or \(\SI{4400}{N}\), and the density of air, \(\rho = \SI{1.21}{kg/m^3}\). But we don’t know the cross-sectional area \(A\) and drag coefficient \(C\) of the car.

Hmm. That could be a problem.

Fortunately, there’s a way around that. Ever heard of a drag race? That’s where you set a car (or two) at the beginning of typically a quarter mile track and just floor it to see how fast it makes it to the end. Besides being good for a movie or two… or six (come on, seriously?), the quarter-mile run is a pretty common way to test a car’s performance, and the results of some of these drag tests are available online. For the ‘67 Impala, the site gives

1967 Chevrolet Impala SS427 (CL)
427ci/385hp, 3spd auto, 3.07, 0-60 - 8.4, 1/4 mile - 15.75 @ 86.5mph

This means the car’s acceleration is sufficient to take it from rest to \(\SI{60}{mph}\) in \(\SI{8.4}{s}\), and that it completed the quarter mile in \(\SI{15.75}{s}\), traveling \(\SI{86.5}{mph}\) over the final 66 feet.

Let’s now go back to the rewritten version of Newton’s second law for a normal car,

You can solve this by rearranging and integrating it, but I’m lazy: I just plugged it into Mathematica. The solution for speed as a function of time is

where \(v_0\) is the initial speed. Now, a ‘67 Impala has a mass of \(\SI{1969}{kg}\) (it varies from car to car, of course, but that’s a representative value), and in a drag test, the initial velocity \(v_0 = 0\). That leaves two variables still unknown: \(F_\text{drive}\), the net forward force which moves the car (engine minus friction), and \(v_T\), its terminal velocity. Luckily, we have two data points we can use to solve for them: the 0-60 benchmark \(v(\SI{8.4}{s}) = \SI{60}{mph}\), and the quarter mile time \(v(\SI{15.75}{s}) = \SI{86.5}{mph}\). Those two velocity-time coordinates should be enough to determine \(F_\text{drive}\) and \(v_T\). Probably the easiest way to do it is to make a contour plot showing the combinations of \(v_T\) and \(F_\text{drive}\) that satisfy each condition, like this:

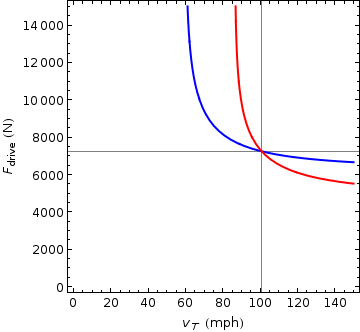
The blue curve shows the points at which

and the red curve shows points where

Their intersection is the one set of parameters that satisfies both conditions, namely \(v_T = \SI{100.8}{mph}\) and \(F_\text{drive} = \SI{7250}{N} = \SI{1628}{lbf.}\). Bingo! Now we’ve got everything we need to calculate the behavior of the rocket car.

Well, wait a minute. We said — actually, Mythbusters said (and what I can find online seems to confirm) that a JATO provides a thousand pounds of thrust. But the value we found for \(F_\text{drive}\) is even larger. Surely a standard car engine can’t be more powerful than a rocket, can it?

I think we have to conclude that it is. Though this isn’t quite what you’d call a standard car engine. The results of the drag test we used to calculate \(F_\text{drive}\) were for the ‘67 Impala SS (Super Sport) 427, a special high-performance version of the car whose engine could crank out \(\SI{385}{hp}\). A standard version of the car would have a less powerful engine, ranging down to \(\SI{155}{hp}\), and thus could have as little as half the engine force — roughly, \(F \propto P^{2/3}\), because \(F \sim v^2\) and \(P = Fv\), and \((150/385)^{2/3} \approx 0.5\).

Note that if you use \(F_\text{drive}\) as obtained from the drag test to calculate the power at the car’s top speed of \(\SI{86.5}{mph}\), you get \(\SI{376}{hp}\), which is quite close to the engine’s reported horsepower. But I think that’s just a coincidence. The same method applied to the car’s eventual top speed of \(\SI{100.8}{mph}\) gives \(\SI{437}{hp}\), which is more power than the engine is even able to generate! This reflects the fact that the way we derived \(v(t)\) makes a lot of simplifying assumptions. For example, it assumes that the air resistance is proportional to \(v^2\). In reality, a car is a complicated shape that induces some amount of turbulence, making the drag force difficult to characterize. More importantly, we’ve assumed the drive force is constant, which is not at all true for a real car. The engine force changes as the car shifts gears and as parts warm up, there are other assorted forces at work like rolling friction.

As a check of sorts on how close this model comes, I’m going to integrate the formula again, to get a formula for distance traveled over time:

In theory, we should be able to plug in the values we found — \(m = \SI{1969}{kg}\), \(v_T = \SI{100.8}{mph}\), and \(F_\text{drive} = \SI{7250}{N}\) — along with the quarter mile time, \(t = \SI{15.75}{s}\), and the distance \(\SI{0.25}{mile}\) will pop out. When I actually plug the values in, I get \(\SI{0.229}{mile}\), which is within 10%, so not bad. That suggests that the different inaccuracies cancel out to some extent.

OK, so where does that leave us? We have a formula,

which seems to somewhat accurately describe the motion of a car under its own power in a drag test. We also have best-fit values for the parameters of this formula: \(v_T = \SI{100.8}{mph}\), and \(F_\text{drive} = \SI{7250}{N}\) for the SS427, and \(F_\text{drive} \approx \SI{3600}{N}\) for a standard Impala. Time to ramp it up to the JATO rocket car!

You may remember from earlier in this post that the terminal velocity is proportional to the square root of the net constant force \(F_\text{drive}\) applied to move the car. If a terminal speed of \(\SI{100.8}{mph}\) corresponds to a drive force of \(\SI{7250}{N}\), then adding on a JATO’s thrust of an additional \(\SI{1000}{lbf.}\) would naively give a terminal speed of

Doing the same calculation for the \(\SI{1500}{lbf.}\) hobby rockets the Mythbusters used gives

which is considerably less than the estimate of a top speed around \(\SI{190}{mph}\) for the car in the pilot episode. Huh.

OK, so what could be wrong with the model?

• Could the drag coefficient — actually the product \(CA\rho\) — of the car (with attached rocket) be much smaller than we thought, making the car’s terminal speed higher? It’s hard to see how. After all, the terminal speed we calculated was for a stock Impala, a shape which is reasonably aerodynamic, but the Mythbusters went and put a rocket pack on it, breaking the airflow over the roof. If anything, it should go slower with the rockets on top.
• Could the car’s engine be more powerful than we think? Again, probably not. I’m already using a value which corresponds to one of the most powerful engines available at the time — it’d still be a pretty strong engine in the modern market. To increase the car’s terminal speed up to \(\SI{190}{mph}\) by increasing engine force would require an engine almost three times as strong as what I’m using in the model.
• What about power losses in the drivetrain? Well, of course those make the car’s terminal speed slower, not faster. There are plenty of reasons to imagine that the terminal speed should be less than what we calculated, but not higher.

I’m actually doubtful that whatever the error is has anything to do with the car itself. Here’s why: suppose we take that equation for \(v(t)\) from earlier and plot it, starting at \(\SI{80}{mph}\), for several different configurations.

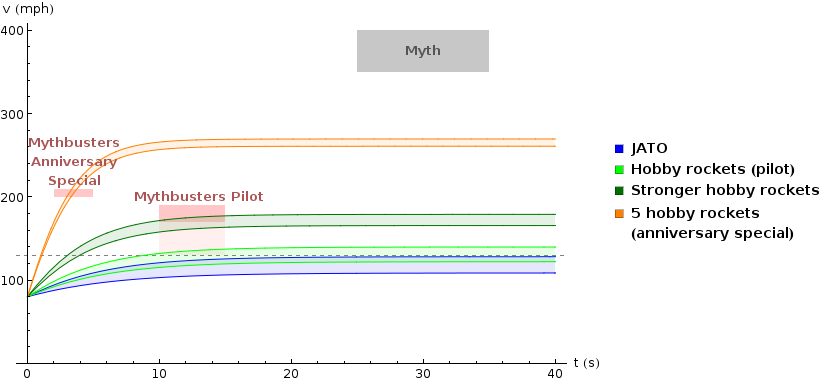
The lower edge of each band represents a car with a standard \(\SI{155}{hp}\) motor, and the higher edge represents a car with an enhanced performance \(\SI{385}{hp}\) motor. And the shaded areas represent the results we actually saw on Mythbusters (or the circumstances described in the myth, for the gray box). Notice that the orange band, representing the car with 5 rockets simultaneously firing as in the anniversary special, goes right through the pink box representing the speed we saw on that show. So the model works in that case!

On the other hand, the light green band, the one for the hobby rockets used in the pilot, only barely breaks the \(\SI{130}{mph}\) speed of the chase helicopter (the dotted line) and doesn’t ever get up to the speed estimate of \(\SI{190}{mph}\). The only way I can come up with to reconcile this math with the results we saw on the show is that the rockets they used might have been more powerful than claimed. If you assume that the rockets give off a little more than twice as much thrust as was said on the show, i.e. around \(\SI{3500}{lbf.}\), you get the dark green curve which seems to come close to the observed results. If anyone knows a better explanation for that difference, I’d be interested to here it, but for now I just have to conclude that something was off about those reported rocket numbers.

Of course, let’s not forget the real point of the graph. None of these curves come anywhere close to the circumstances claimed in the myth! So despite the discrepancies in the details, the conclusion remains solidly the same: physics says this myth is absolutely busted.