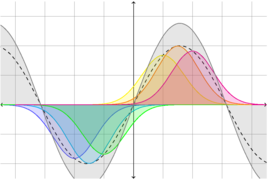
One of the neat properties of the Fourier transform is that if you want to convolve two functions, an easy way to do it is to multiply their Fourier transforms together and then take the inverse Fourier transform of the result. It’s often said as “convolution in normal space corresponds to multiplication in Fourier space.” I think I’ve always accepted this on faith, but today I had occasion to actually come up with a proof.

To start with, let’s make some definitions. The convolution of two functions \(f(x)\) and \(g(x)\) is the result of shifting and scaling one function by each point of the other. It’s usually used in applications where one of the functions is a Gaussian distribution, or some other function that has a peak at some point, and in that case you can think of it like this: suppose \(g(x)\) is the function with the peak. For each point \(\bigl(y,f(y)\bigr)\), make a copy of \(g(x)\), and shift it over so that the peak is at \(y\). Then multiply it by the value of \(f(y)\). The sum of all those scaled and shifted peaks is …