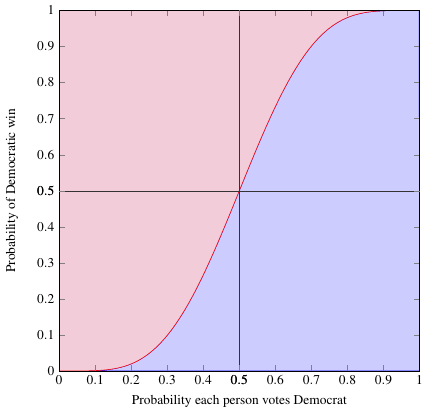
It’s Election Day (in the US), and I have a relevant post I’ve been meaning to do for a while.

Suppose you have a binary experiment, one which has two possible outcomes with probabilities \(p\) and \(q = 1-p\). For example, voting. (Pretend there are only 2 parties) Overall, let’s say people vote Democrat with probability \(p\) and Republican with probability \(q\). Now suppose a large number \(N\) of people all go out to vote; what can you say about the results?

In a statistical experiment like this, the possible results are drawn from a binomial distribution, in which the probability of getting \(n\) Democratic votes (and \(N - n\) Republican) is

The probability that the Democrats will come out ahead is just the sum of all the probabilities for all the outcomes where \(n\) is more than half of the total vote: we start at \(n = \floor*{\frac{N}{2} + 1}\), which is the first integer greater than \(\frac{N}{2}\), and add up probabilities all the way to \(n = N\).