Like everyone else, I feel a need to analyze the giant water slide in the latest Mythbusters episode. But honestly, there isn’t much left to say. The original video has been around for a while and everybody else who does this kind of analysis has already had the chance to do it. Example 1; example 2 (okay, so I’m only linking to one blog, but there must be more).

I guess I might as well do the obvious calculation, but I’ll use the Mythbusters’ parameters instead of those from the original video (which are unknown). The slide starts with a downward ramp $\unit{165}{\foot}$ long at a $\unit{24}{\degree}$ slope, which then curves upward to a $\unit{30}{\degree}$ launch ramp that terminates $\unit{12}{\foot}$ above the surface of the lake. They didn’t say how long the launch ramp is, but I can work without that information. I’ll be trying to calculate two quantities mentioned on the show: how far each Mythbuster flies from the end of the ramp, and his maximum speed.

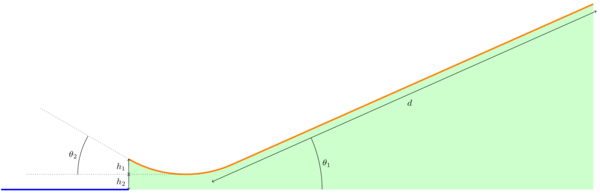
(here’s a full-size version)

There are two parts to this problem:

1. The slide
2. The flight

The first part is an energy problem. All energy problems can be solved in the same way, starting with the work-energy theorem

and plugging in, term by term.

$W_\text{ext}$ is the work done by external, nonconservative forces, like friction. The friction is proportional to the normal force, which (for most of the slide) is in turn equal to the component of gravity acting perpendicular to the surface. So

where $\theta_1$ is going to be the $\unit{24}{\degree}$ angle of the acceleration ramp. This frictional force acts antiparallel to the motion over a distance of $d\equiv\unit{165}{\foot}$ (plus a little correction that I’ll leave for later), so we get

The next term, $E_f$, is the final energy, at the end of the slide when the person flies off. This is a combination of gravitational potential energy, $U = mgh$, and kinetic energy, $\frac{1}{2}mv^2$. Accordingly, I’ll write it

using $h_1$ to represent the height of the launch point above the lowest part of the ramp.

Finally, the initial energy is purely gravitational. The height is a lot higher this time; specifically,

Putting it all together,

The first thing to notice is that mass cancels out, so it shouldn’t make a difference how heavy you are. In the show, Jamie flew 2 feet further than Adam, but I suspect that that was just a fluke, not a statistically significant result. I get

By the way, this factor of $\sin\theta - \mu_k\cos\theta$ seems to be fairly common — you can often expect to see it when doing a problem that involves a ramp with friction.

Now it’s time to move on to part 2, which is a projectile motion problem. I’ll use the same height reference as before, the bottom of the curve of the ramp. So we’re launching an object from height $h_1$ at an angle $\theta_2$ to a surface at height $-h_2$; how far does it travel?

First step: Find the time it takes to hit the water.

Plugging in the relevant expressions, we get

which has the solution

Second step: multiply that time by horizontal velocity to get horizontal distance. This one is easy; the horizontal velocity is $v\cos\theta_2$ so we get

Given that the solution for the previous part came out in terms of $v^2$ (because I dislike ugly square root signs), here’s a useful way to rewrite that:

At this point we could substitute in $v^2$ from before and get a symbolic expression, but it’s getting pretty complicated. Probably better to plug in numbers.

First, a recap of the numeric values involved. I’m taking the length of the slide from the top down to its lowest point to be $d = \unit{165}{\foot}$, the height of the end of the slide above that lowest point to be $h_1 = \unit{6}{\foot}$, the height of the water below the lowest point of the slide to be $h_2 = \unit{6}{\foot}$, and the angles of the slide and the launch ramp respectively to be $\theta_1 = \unit{24}{\degree}$ and $\theta_2 = \unit{30}{\degree}$. Plugging all these in to the expression for velocity, I get

Hmm, well that’s a problem. Or is it? We don’t know the coefficient of friction, but we do know the number this is supposed to work out to, namely $(\unit{30}{\mileperhour})^2$. The value $\unit{30}{\mileperhour}$, was given on the show as the maximum speed reached by both Jamie and Adam as they went down the slide. Technically my expression for velocity is for the speed at the end of the launch ramp, which will be a little slower than the maximum speed, but I’ve made enough approximations that it probably doesn’t make a big difference. So I’ll go ahead and plug in $v = \unit{30}{\mileperhour}$ and use Mathematica to solve for the coefficient of friction, $\mu_k$. It comes out to be $\mu_k = 0.2$. Seems reasonable.

Let’s try this another way, though. Again using Mathematica, I can substitute my expression for $v^2$ into the expression for $x$. Both Jamie and Adam flew about $\unit{70}{\foot}$ horizontally, so that’s my value for $x$. Then I can plug in all the other distances and angles taken from the show and get another equation for $\mu_k$:

That one takes a bit more algebra — of course, I’ll just get Mathematica to do it ;-) The solution works out to… $\mu_k = 0.2$! The fact that these two values are the same is, at least, an encouraging sign that this calculation actually corresponds to reality.

Here’s something else we can try: predicting (actually “postdicting”) the distance covered on each of the earlier, shorter slides. Everything (including the coefficient of friction) is the same as before, except for the distance $d$, which was first a half, then three quarters, of the total length. So if I plug in $d = \frac{1}{2}\times\unit{165}{\foot}$, I get

Not so great, considering that the actual distance Adam flew on that run was just 4 feet. But the corrections I alluded to earlier might help that out a bit… that’s a story for another post, though. What about $d = \frac{3}{4}\times\unit{165}{\foot}$?

They didn’t give measurements for these runs on the show, but from the video I estimate that Adam flew about 40 feet. Still not that great, but we’re getting closer.

Even though I know this model doesn’t quite work, I’ve got one last set of numbers to run. How high would the ramp have to be to achieve the hypothetical $\unit{115}{\foot}$ flight in the video? Since I already had the Mathematical machinery set up to compute flight distance for a given ramp length, I decided to do this one by trial and error, plugging in different values for $d$ to narrow in on the one that yields a distance of $\unit{115}{\foot}$. It works out to $\unit{85}{\meter}$, or $\unit{280}{\foot}$, which is really long. But think about this: for shorter runs than the Mythbusters’ full-length slide, my model overestimates the distance traveled. Perhaps for longer runs, it’ll underestimate the distance traveled, which means that in reality, maybe a shorter slide would do the job. And in fact, if you look at the data points for the slides on the show — keeping in mind that it’s dangerous to extrapolate from only three points — they do seem to fall in a line, and that line suggests that you might only need a $\unit{220}{\foot}$ slide to achieve a $\unit{115}{\foot}$ flight.

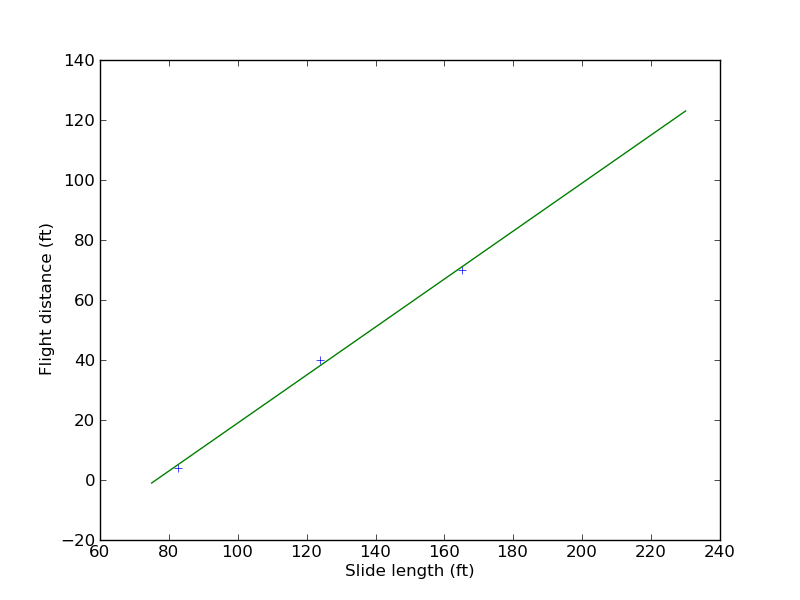
Interesting, isn’t it?