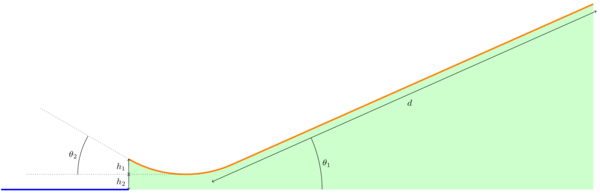
Like everyone else, I feel a need to analyze the giant water slide in the latest Mythbusters episode. But honestly, there isn’t much left to say. The original video has been around for a while and everybody else who does this kind of analysis has already had the chance to do it. Example 1; example 2 (okay, so I’m only linking to one blog, but there must be more).

I guess I might as well do the obvious calculation, but I’ll use the Mythbusters’ parameters instead of those from the original video (which are unknown). The slide starts with a downward ramp \(\unit{165}{\foot}\) long at a \(\unit{24}{\degree}\) slope, which then curves upward to a \(\unit{30}{\degree}\) launch ramp that terminates \(\unit{12}{\foot}\) above the surface of the lake. They didn’t say how long the launch ramp is, but I can work without that information. I’ll be trying to calculate two quantities mentioned on the show: how far each Mythbuster flies from the end of the ramp, and his maximum speed.

(here’s a full-size version)

There are two parts to this problem:

1. The slide
2. The flight

The first part …

It’s finally time to analyze the latest Mythbusters episode again. This one has Grant, Tory, and Jessie testing another myth about that bus from the movie Speed. According to the Mythbusters, in the movie the bus, traveling at 70 miles per hour, was able to jump over a 50 foot gap in the highway, land safely, and continue on its way.

There’s an obvious physics question in here: could the bus even make the jump? Well, while it’s in the air, the bus is basically just a projectile, and projectile motion is one of the most basic topics in physics. This shouldn’t be hard to calculate. The equation for uniformly accelerated motion in one dimension is

In a two-dimensional system, like a flying bus (up and forward: two dimensions, assuming it doesn’t move sideways), we use two of these equations, one for each dimensions. And if we ignore icky things like air resistance, it’s easy to determine each of the individual factors in the equation:

• Let’s choose coordinates such that \(x_0 = 0\) and \(y_0 = 0\), setting the edge of the road where …