Death rays and thermal radiation

Posted by David Zaslavsky on December 11, 2010 8:26 PM

— Comments

It’s been far too long since I did a Mythbusters writeup, but I think it’s time to stop stalling and bring this series back. On this week’s episode, Adam and Jamie tested the myth of Archimedes’ heat ray for a third time — that has to be some kind of record — at the request of President Obama.

The gist of the myth is this: by focusing enough of the sun’s rays, using a large number of mirrors, on an enemy ship, the Greeks hoped to heat it up enough to make it catch on fire. So far (spoiler alert), there’s no evidence that this thing ever could have worked. All three of the Mythbusters’ tests have failed.

But I think I can shed some light (no pun intended) on why. As it happens, I taught a lab on thermal radiation transfer this week, and that (along with an interesting perspective on gravitationally baking a turkey) reminded me that it’s fairly straightforward to calculate, at least in a simple model, the amount of radiation it takes to heat something up to a particular temperature. It all stems from the Stefan-Boltzmann equation,

$$P = \sigma\epsilon AT^4$$

This equation actually serves a dual purpose: it tells you the rate at which an object at temperature $T$ loses energy due to thermal radiation alone (not counting other effects like heat conduction), and it also tells you the rate at which an object in an environment at temperature $T$ gains energy from that environment, again due to thermal radiation alone. In either case, $\sigma$ is the Stefan-Boltzmann constant, $A$ is the object’s surface area, and $\epsilon$ is the object’s emissivity. Since any real object will be both emitting and absorbing radiation, the two uses of the equation are often combined to give the net power loss due to thermal radiation:

$$P = \sigma\epsilon A(T^4 - T_0^4)$$

Here I’m using $T_0$ to designate the temperature of the environment, and plain $T$ is the temperature of the object.

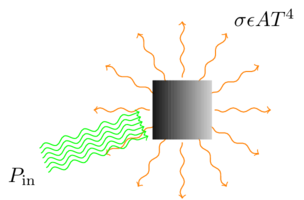
So here’s the simple model. Suppose that the piece of the ship you’re trying to set on fire is effectively insulated, so that it doesn’t gain or lose heat by conduction. (The parts of a ship that you’d try to set on fire, the sails or perhaps the wooden hull, generally don’t conduct heat very well; besides, the problem gets a lot harder if you relax this assumption.) The piece will lose energy through thermal radiation, at a rate determined by the equation above, and it will gain energy from the sunlight being focused on it. When it’s at thermal equilibrium (which it essentially always is), those two will be equal,

$$P_\text{sun} = \sigma\epsilon A(T^4 - T_0^4)$$

If the equilibrium temperature $T$ is greater than or equal to the flash point of the material, it catches on fire. Simple enough.

The final piece of the calculation involves figuring out the power input from sunlight. This is just going to be the solar irradiance $I$, representing the power of sunlight per unit area, times the area $A_\text{mirror}$ of the mirrors used to reflect the light, times the cosine of the angle of incidence of the sunlight, times the reflectivity of those mirrors, $\rho$.

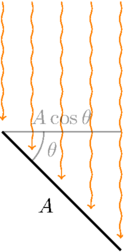
But to get the amount of this sunlight that actually reaches the sail, we need to throw in a couple of extra factors. First, since the aiming of the mirrors is not perfect, we’ll need a number $n$ representing the fraction of mirrors that were actually reflecting their light to the right place. Also, since some of the radiation reaching the sail will be reflected, only a fraction of it actually goes towards heating the sail, so we need to multiply in the absorptivity $\mathcal{A}$ of the sail’s material. Putting it all together, we come up with this expression,

$$P_\text{sun} = In\mathcal{A}\rho\cos\theta A_\text{mirror}$$

giving the following for the area of mirrors required:

$$A_\text{mirror} = \frac{\sigma\epsilon A_\text{target}}{In\mathcal{A}\rho\cos\theta}(T_f^4 - T_0^4)$$

So it’s time to plug in some numbers.

Let’s start with the Mythbusters’ most recent test:

They used a square patch of sail $\unit{50}{\inch}$ on a side, with an area of $A_\text{target} = \unit{1.61}{\meter^2}$.
We were told in the show that the flash point of the sail was $\unit{410}{^{\circ}F}$, or $T_f = \unit{483}{\kelvin}$.
The initial temperature of the sail was reported as $\unit{85}{^{\circ}F}$, or $\unit{303}{\kelvin}$ (although this number is not going to matter much once you take the fourth power).
We don’t know the angle of incidence for the incoming sunlight on the mirror, but it’s possible to estimate it by measuring the tilt of the mirrors from the episode, knowing that the rays were being reflected on to a pretty much horizontal path. I come up with an estimate of $\unit{0.4}{\radian}$ (that’s around $\unit{23}{\degree}$); perhaps it was a little more in reality.
To get the solar irradiance, I integrated the direct ASTM reference spectrum, coming up with a value of just about $\unit{1}{\frac{\kilo\watt}{\meter^2}}$.
From Wikipedia, I find that the reflectivity of an aluminum mirror, which is a fairly common modern design, is around $\rho = 0.9$.
Another reference listed on Wikipedia gives the emissivities of various sorts of black paint in the range $\epsilon \sim 0.9$.
Yet another reference (found by a random Google search) shows that the absorptivities of many black paints are in the vicinity of $\mathcal{A} \sim 0.9$. (no surprise there…)
Since I’ve been making optimistic assumptions so far, I might as well continue that trend by going with $n = 0.8$: 80% of the mirrors are correctly aligned to reflect on to the target.
Finally, the Stefan-Boltzmann constant has a numerical value of $\snunit{5.67}{-8}{\frac{\watt}{\meter^2 \kelvin^4}}$.

Plugging in all the numbers, I come up with $\unit{6.5}{m^2}$ for the required surface area of the mirrors.

Hm… that’s not very much. The 500 mirrors would have had no problem setting the boat on fire. Clearly something is wrong with this calculation. A couple of things come to mind almost immediately: perhaps the absorptivity of the sail was actually lower, so that it reflected more sunlight. Perhaps its emissivity was higher, so that it was more efficient at radiating away excess energy. Perhaps the fraction of mirrors on target was lower than $0.8$ (and I can’t really blame the kids, those mirrors were nearly as big as some of them were).

Digging a little deeper, it’s possible that the attenuation of sunlight by the atmosphere was more than the ASTM spectrum accounts for, although I wouldn’t expect this to have been a big issue. The ASTM spectrum models the radiation received when the sun is about $\unit{42}{\degree}$ above the horizon, and based on my observations from the show, the sun was pretty close to that inclination when they did the experiment. Admittedly the pressure, humidity, etc. at the test site were certainly different from the ASTM reference values, but again, I don’t see that making a huge difference.

Another thing to consider is that several of the values I included in the formula are actually wavelength-dependent, namely emissivity, absorptivity, and reflectivity, as well as the spectral irradiance from the sun. So the incoming power should really be expressed as a function of the wavelength of the light and the angle,

$$P_\text{sun}(\lambda) = I(\lambda)n\mathcal{A}(\lambda)\rho(\lambda)\cos\theta A_\text{mirror}$$

The same goes for the thermal equilibrium condition, although it’s still the total power that determines whether the temperature changes,

$$\int\frac{P_\text{in}(\lambda)}{\epsilon(\lambda)}\udc\lambda = \sigma A(T^4 - T_0^4)$$

Putting these together makes the mirror area formula look much more complicated:

$$A_\text{mirror} = \frac{\sigma A_\text{target}\cos\theta}{n}(T_f^4 - T_0^4)\biggl[\int\frac{\epsilon(\lambda)\udc\lambda}{I(\lambda)\mathcal{A}(\lambda)\rho(\lambda)}\biggr]^{-1}$$

But usually, it’s reasonable to approximate the functions of $\lambda$ as constant over the range of wavelengths we’re dealing with, so I doubt that this would account for the two-orders-of-magnitude error in my result. (If you have access to a lot of data on optical properties of various materials, feel free to plug this thing into a computer and find a value for it to see whether that’s in fact the case.)

Honestly, though, I think the biggest problem the model doesn’t work is that I completely ignored other ways in which heat is removed from the target. Specifically, heat loss to the surrounding air is likely to be a major factor, because convection can carry away a lot of energy. I’m going to say that working out exactly how fast energy is lost this way is “beyond the scope of this post” — that is, either impossible or more work than I have time for ;-) But we can make a quick estimate by modifying our equation to include a generic heat loss term,

$$P_\text{sun} - P_Q = \sigma\epsilon A(T^4 - T_0^4)$$

Plugging in the other formulas from before, I get

$$P_Q = In\mathcal{A}\rho\cos\theta A_\text{mirror} - \sigma\epsilon A_\text{target}(T^4 - T_0^4)$$

Now, with the numbers previously estimated and using $\unit{500}{\meter^2}$ for the total area of all the mirrors (should be within a factor of 2, right?) gives

$$P_Q = \unit{294}{\kilo\watt}$$

That’s kind of a lot. Wait — is it a lot? Well, if you calculate the total power that should be coming in from the sun, you get $P_\text{sun} = \unit{298}{\kilo\watt}$ (and I think that formula can be trusted). So if this is correct, the sail is incredibly efficient at radiating away the energy it receives from sunlight; a mere 1% of the incident energy in this situation actually goes into heating it up! No wonder it’s such a hard thing to pull off.