Again entering the realm of interesting physics from last month: a group of scientists proposed a new and quite promising explanation for the Mpemba effect, the observation that warmer water sometimes freezes faster than colder water.

The Definition

Oddly enough, even though the Mpemba effect has been known since ancient times, and its namesake paper was published over half a century ago, physicists can’t even seem to agree on a precise definition of the effect. What we know is that, if you take two containers of water (or, evidently, a water-based mixture like milk) which are identical in every respect except that one is at a higher temperature than the other, and you put them both in a freezer, under some conditions the one at the higher temperature will freeze before the one at the lower temperature. But what conditions are those? And what exactly does it mean to freeze first? Freezing is an extended process, after all; is it talking about when the water reaches zero degrees (Celsius), or when it begins to form ice, or when it is completely converted into ice, or something else?

Part of the contribution of this new paper is a proposal of a new way to define the Mpmeba effect. Rather than focusing on the time taken for a sample of water to actually freeze (with all the ambiguity in the definition of “freeze”), they frame it in terms of the instantaneous rate of change of the water’s temperature. According to Newton’s law of cooling, the rate at which a substance cools is related to the temperature difference between it and its surroundings, by the equation

Here \(\Delta T\) is the temperature difference between the substance and surroundings, and \(-\ud{\Delta T}{t}\) is the rate of cooling. (The derivative \(\ud{\Delta T}{t}\) is negative because the thing is cooling, so the minus sign makes it into a positive value.) The constant \(\tau\), called the relaxation time in the new paper, can be thought of as the ratio of the temperature difference to the instantaneous cooling rate:

A sample that cools faster will have a shorter relaxation time \(\tau\). In this new paper, Zhang et al use \(\tau\) to define the Mpemba effect: the assertion is that water that starts at a higher temperature has a lower \(\tau\).

Of course, this is all theory. You might ask what if water doesn’t even follow Newton’s law of cooling? Well, not to worry, they show that it does:

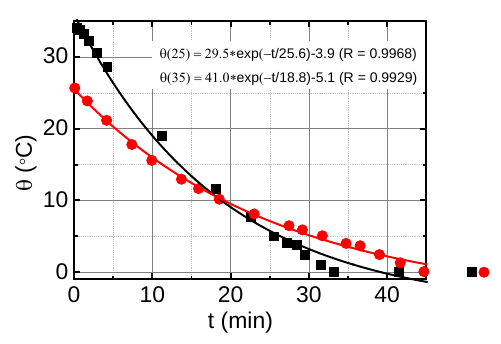
When you solve the differential equation above, you get

The scientists tried to fit this exponential formula to the data shown in the image above. As you can tell, it matches fairly well, which shows that the water samples do obey Newton’s law, and also allows them to obtain a value for \(\tau\): for the water that started at 25 degrees, \(\tau = \SI{25.6}{min}\), and for the water that started at 35 degrees, \(\tau = \SI{18.8}{min}\). Clearly the Mpemba effect in these particular samples is real!

The Explanation

As you might guess, if physicists can’t even define the Mpemba effect, they’re not even close to agreeing on an explanation for why it happens. Not for lack of trying, of course. People have proposed many different mechanisms over the years; for example, as listed in the Wikipedia article:

• Evaporation at the higher temperature reduces the mass of water in the sample
• Convection is increased at high temperatures, leading to more rapid cooling
• Lower temperature water freezes from the top, insulating it from further cooling, whereas higher temperature water freezes from the bottom and sides
• Colder water is more susceptible to supercooling, which would increase the time it takes to turn into ice
• Heating water removes dissolved materials that lower the freezing point and change the specific heat, which changes the rate of cooling
• Hot water is more able to melt through a layer of frost in the freezer itself

Honestly, most of these explanations seem like a stretch to me. They tend to be based on weird behavior of water while it freezes, whereas the new paper by Zhang et al shows that the Mpemba effect actually has nothing to do with freezing. You can see it in action while the water is well above zero degrees.

Consider this: the sample of water that starts at 35 degrees becomes a 25 degree sample about 6 minutes into the experiment. From that point forward, it takes about 27 minutes to reach zero degrees. But the other sample, which started at 25 degrees, took 45 minutes to reach zero degrees! Clearly, there is something qualitatively different about water that has been sitting at, say, 25 degrees for a while compared to water that was just recently cooled to 25 degrees.

The other main contribution of this new paper is an idea of what that difference might be. Their proposed explanation is all about the behavior of the bonds between hydrogen and oxygen atoms within and between water molecules. Now, this part of the paper is pretty hard to follow, but as far as I can tell, their argument goes like this: you can think of the atoms in two adjacent water molecules as having different kinds of springs between them, representing the interatomic bonds. There’s a strong spring (a covalent bond) connecting the hydrogen and oxygen in one molecule, and a weak spring (a hydrogen bond) connecting that hydrogen to the oxygen atom in the next molecule.

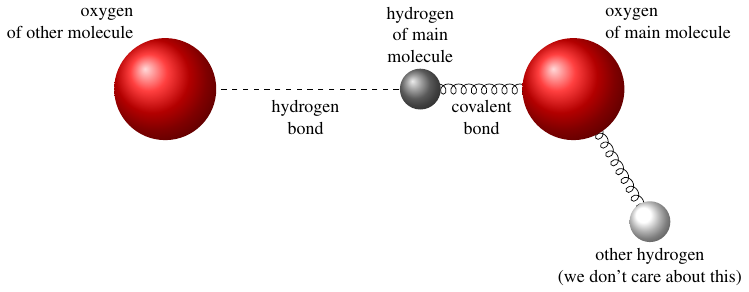
We can model these springs (bonds) using their potential energy functions: the curves in this next picture show how the potential energy varies as each oxygen atom gets closer to or further from the hydrogen atom.

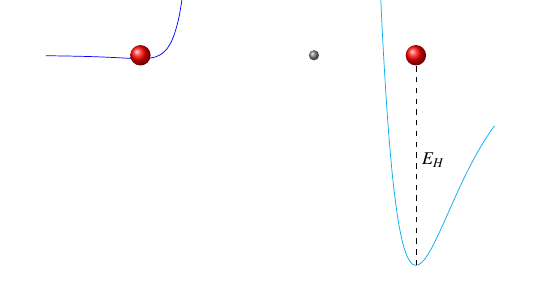
The covalent bond, on the right, has a steep potential energy function, which means it takes a lot of energy to change that atom’s position by just a tiny bit. Conversely, the hydrogen bond has a nearly flat potential energy function, which means it doesn’t take much energy to move that atom by a significant distance.

It turns out that, in hotter water, the natural lengths of the bonds change such that the covalent bond gets a little shorter and the hydrogen bond gets a bit longer.

I’ve exaggerated the effect in that picture; it’s actually a very small change. This next plot shows how the potential curves change using actual numbers from the paper:

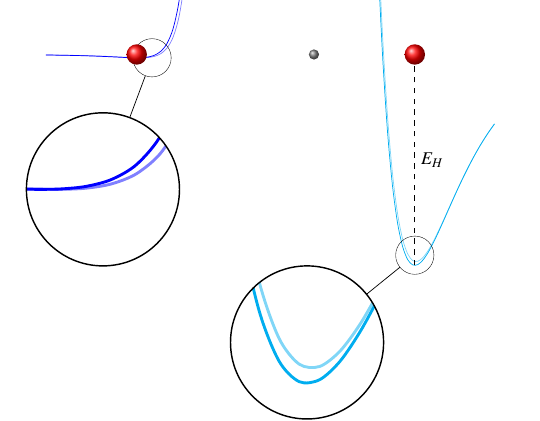
The dark lines represent the potential energy curves for water that starts at 90 degrees Celsius, and the lighter lines represent the potential energy functions at 40 degrees Celsius. It’s barely noticeable, but it is enough to make a distinct difference in the behavior of the water molecules. See, when the covalent bond gets shorter and its potential curve gets deeper, it’s able to store more energy. And when more energy is stored in that bond, according to the paper, the energy gets released faster, which leads to faster cooling.

I have to admit, after spending days staring at this paper, I still can’t wrap my head around how this mechanism is supposed to work. I guess that in water which is only heated to (for example) 25 degrees, the potential curve has a certain depth, whereas in water which is heated to 35 degrees, the potential curve has a greater depth, and keeps that greater depth even as it cools. That would be the sort of qualitative difference that is needed to explain the Mpemba effect. But I just don’t know enough about the behavior of atomic bonds to understand why that would happen, or whether it’s even correct. Readers, if you know how this stuff works, can you fill in the details?

Regardless, the authors of this paper seem to have a solid theoretical prediction. Somehow, they’re able to calculate a relationship between the relaxation time \(\tau\) and a quantity \(\Delta d_H^2\), the change in the length of the covalent bond between the initial temperature and the freezing temperature.

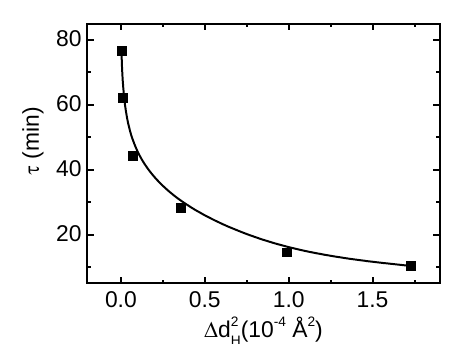
\(\Delta d_H^2\) is proportional to the initial temperature, and thus higher initial temperatures mean shorter relaxation times — precisely what the Mpemba effect is all about. So if all this logic holds up, perhaps they do have the real explanation for this effect at last.