Here’s a tidbit of science that I should have written about a long time ago. Last month, there was a surge of excitement in the particle physics community when the ATLAS detector team announced that they had pretty much conclusively observed the Higgs boson decaying to tau leptons for the first time.

Now, you might be forgiven for thinking “what’s the big deal? I thought we already found the Higgs boson?” Well yes. A year and a half later, physicists are fairly confident that what they found is the standard model Higgs boson. But back in July 2012, when the discovery was first announced, all anyone knew was that ATLAS and CMS had discovered a previously unknown particle with a mass of \(\SI{126}{GeV}\). It wasn’t clear just what kind of particle it was: the standard model Higgs boson, another kind of Higgs boson, or something else entirely. That question would be resolved by gathering more data on how the new particle interacts with other, known particles, and that’s what this most recent bit of news is about.

The Higgs search: a year in review

To understand all this in more detail, let’s back up to about a year ago, when the original discovery of Higgs boson was still hot — well, warm off the presses — and the physics community was awaiting new updates at every conference. You may remember that ATLAS and CMS were searching for the Higgs boson by looking at five channels, or possible ways in which the particle was expected to decay:

• \(H\to\gamma\gamma\) (two photons)
• \(H\to WW\to ll\nu\nu\) (two leptons and two neutrinos)
• \(H\to ZZ\to 4l\) (four leptons)
• \(H\to\tlp\talp\) (tau lepton and antilepton)
• \(H\to\btq\btaq\) (bottom and antibottom quark)

These particular channels were chosen because, out of all the particles a Higgs boson can decay into, these are the easiest to detect.

If you look back to one of my earlier posts showing results from all these channels, you’ll notice that, as of about a year ago, none of the individual channels had been detected enough times to be sure (by the \(5\sigma\) particle physics standard) that the newly discovered boson decayed into those particles. In other words, physicists were not yet ready to conclude for sure that the new particle definitely interacts with W bosons. Or with tau and antitau leptons. But each of these channels individually was detected just a bit more than you’d expect without the Higgs boson, so that when you put them all together, it added up to conclusive evidence of a new particle.

Once we knew there was a new particle there, though, the focus turned to identifying that particle’s properties. There are several properties that needed to be checked to determine whether the particle is really the Higgs boson: among them are spin and parity, which I’ve mentioned before, but this most recent ATLAS result is really about the interaction strengths with other, known particles. (See the image at right for a handy reference, from Wikipedia.)

There are two major kinds of interactions the experiments have been looking for:

• Does the particle interact with bosons? The original Higgs mechanism, which explains why the W and Z bosons have mass, predicts that the Higgs boson interacts with those W and Z bosons. If the new particle didn’t decay to W and Z, it couldn’t be the Higgs boson. We’d be able to tell if this was happening because the number of events seen in the bosonic decay channels — that is, the number of collisions in which either 2 leptons (plus two undetectable neutrinos), or 4 leptons, were detected — would match the predictions of the standard model without a Higgs boson.

  Of course, that’s not what happened. Right from the beginning, when the discovery was first announced in July 2012, the number of events seen in the bosonic channels exceeded what the Higgsless standard model could explain by a fairly significant amount. And in March of this year, the combined results of both ATLAS and CMS for the decay channel \(H\to WW\to ll\nu\nu\) (probably) passed the threshold for discovery. That means we can be essentially sure that the new particle does interact with W bosons, and that more or less confirms its identity as the Higgs boson.

• Does the particle interact with fermions? Although the Higgs mechanism was invented to explain the masses of the W and Z bosons, it can also be adapted to explain how fermions have mass. This “extended Higgs mechanism” predicts that the Higgs boson should interact with those fermions. If the new particle doesn’t interact with the fermions, that means there has to be some other way in which fermions get their mass, and that would be very interesting indeed!

  In order to check whether this “extended Higgs mechanism” is a real thing, we have to look at the numbers of events detected in the fermionic decay channels, \(H\to\tlp\talp\) and \(H\to\btq\btaq\). As with the bosonic channels, if the Higgs boson interacts with fermions, these numbers of events should match the predictions made including the Higgs boson. If it doesn’t, the observed numbers of events should match the smaller predictions made without the Higgs boson. But unlike the bosonic case, the predictions with and without the Higgs boson for fermionic decays are quite close together, and that made it difficult to tell which model matched better. If you look back to the results from a year ago, CMS was only barely able to distinguish between them. What ATLAS announced last month is that they have finally collected enough data to eliminate the Higgsless standard model (i.e. the predictions made without the Higgs boson) at the level of \(4.1\sigma\).

  The almost-discovery that the Higgs boson decays to fermions is important not only in its own right, but also because fermions have spin 1/2. When you put two of them together, you can make a total of spin 0 or spin 1, but not spin 2. So if we see the Higgs decaying to fermions, that means its own intrinsic spin has to be 0 or 1. But we already know that it can’t be spin 1, because the Higgs decays to two photons, or two W bosons — those are spin-1 particles, and only something with spin 0 or 2 can decay to a pair of them. The only possibility that is consistent with both photon decay and fermion decay is that the Higgs boson has spin zero. That was part of the prediction of the Higgs mechanism, so it’s not unexpected, but it is exciting because this is the first spin-0 particle known to exist!

ATLAS Results

Let’s have a look at the actual ATLAS results released last month.

Most of the paper goes through the details of how the detector picks out the events characteristic of the \(H\to\tlp\talp\) channel, which is a pretty complex problem in its own right. Because tau leptons have an incredibly short lifetime, ATLAS can’t detect them directly. Instead, it has to detect the things they decay into. These secondary decays fall into two categories, leptonic (where a tau decays into a muon or electron) and hadronic (where a tau decays into a whole jet of assorted hadrons). Unfortunately, in both cases, there are many other things going on that can produce the same end result, so it takes some complex computer algorithms to try to sort out which electrons or muons or jets come from tau decay and which ones don’t. All the discussion of boosted decision trees, kinematic reconstruction, preselection, and so on is about that. I’m just going to skip over it.

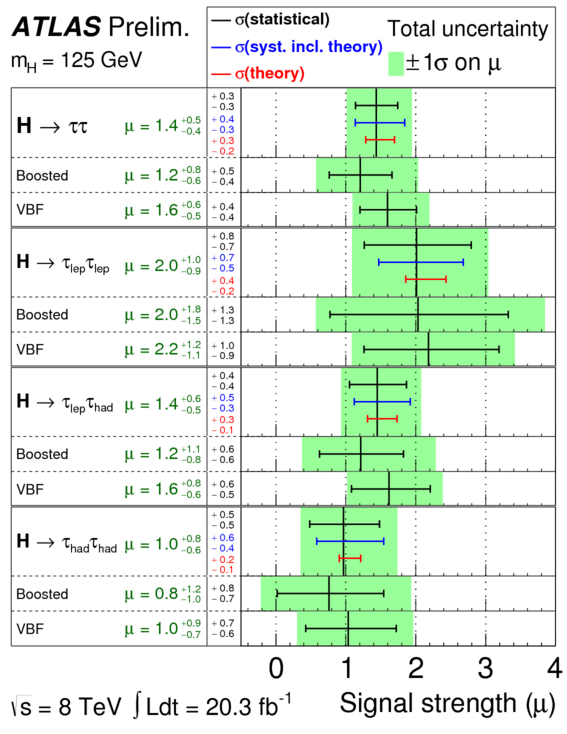
What I’m more interested in for purposes of this blog post are the final results, as shown in figure 9 from the ATLAS paper:

This shows the most likely values of the signal strength parameter \(\mu\), defined as

The cross section \(\sigma^{pp\to H}\) is a measure of how often a Higgs boson is produced in a collision between two protons, and the branching ratio \(BR^{H\to\tau\tau}\) is the fraction of Higgs bosons which decay into tau and antitau leptons. So this signal strength \(\mu\) basically indicates how often the Higgs tau tau decay actually happens relative to how often it’s predicted to happen. If \(\mu = 1\), that means the decay happens exactly as often as the standard model predicts. If \(\mu = 0\), that means it doesn’t happen at all. Based on the figure above, in the very top row, you can see that it actually happens even more than expected: the most likely value after putting all the different pieces of evidence together is \(\mu = 1.4\).

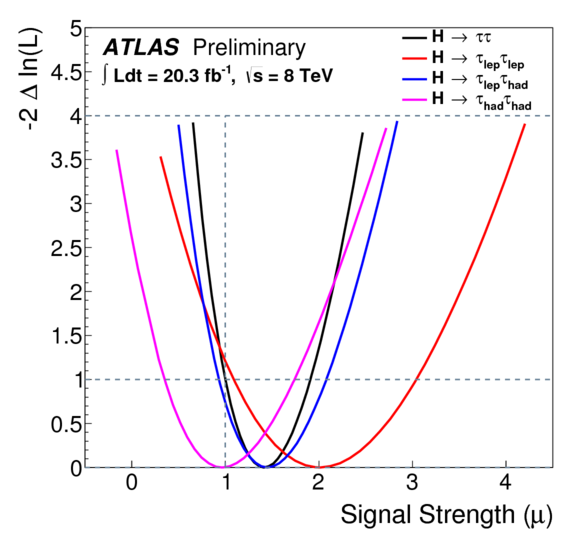
The paper also includes a log likelihood plot in figure 10:

which should look very familiar if you read my post about Tesla fires and statistics! This graph is useful because it lets us see just how strongly the ATLAS results exclude the possibility that the Higgs doesn’t decay to tau leptons at all. That possibility corresponds to \(\mu = 0\). So, as I explained in my Tesla statistics post, you can look at the black curve which represents the log likelihood of the data, follow it up to see where it crosses the vertical line corresponding to \(\mu = 0\), and… well, it runs off the top of the plot. Fortunately, they give us the number: 4.1 standard deviations, which means the black curve crosses \(\mu = 0\) at \(-2\Delta\ln\mathcal{L} = 4.1^2 = 17\). That’s pretty high! It’s not quite up to the \(5\sigma\) threshold (that’d be \(-2\Delta\ln\mathcal{L} = 25\)) that we call a discovery, but it does mean it’s quite likely that the Higgs boson decays to tau leptons. I wouldn’t be surprised if CMS is currently crunching some numbers that, when combined with the ATLAS result, will show conclusively that the \(H\to\tlp\talp\) decay is happening, and thus that the Higgs field also gives mass to fermions.

In one sense, this is an exciting discovery, because it neatly wraps up some outstanding questions about the nature of mass and the role of the Higgs boson. We are now fairly sure that the Higgs mechanism gives mass to all the known fundamental particles that have any mass at all. (I guess there’s still the option of Majorana neutrinos, but that’s an entirely different story.) On the other hand, it’s kind of disappointing. The fact that physics is behaving exactly the way it was predicted to cuts off a lot of theoretical predictions of new things that might have been discovered. The particle physics community will just have to continue waiting to find the next new and exciting phenomenon.