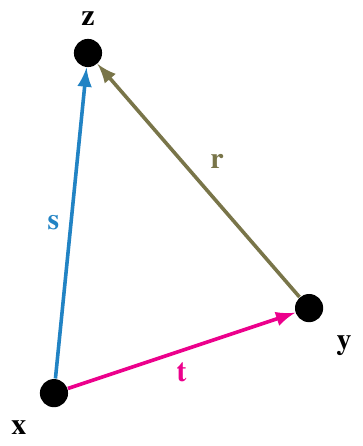
Just a quick mathematical observation for today (actually yesterday): suppose you have three points. Any function of the three points which doesn’t depend on their absolute location or orientation only depends on the magnitudes of the vectors joining the three points.

Suppose the three points are \(\mathbf{x}\), \(\mathbf{y}\), and \(\mathbf{z}\). A function that doesn’t depend on the absolute location of the points will only depend on the displacements between them, \(\mathbf{r} = \mathbf{z} - \mathbf{y}\), \(\mathbf{s} = \mathbf{z} - \mathbf{x}\), and \(\mathbf{t} = \mathbf{y} - \mathbf{x}\). And a function that doesn’t depend on the orientations will only depend on the scalar quantities we can form out of these displacements: \(r^2\), \(\mathbf{r}\cdot\mathbf{s}\), \(s^2\), \(\mathbf{s}\cdot\mathbf{t}\), \(t^2\), and \(\mathbf{t}\cdot\mathbf{r}\). But the dot products are actually not independent, because for example

so,

Then you can write \(\mathbf{r}\cdot\mathbf{s} = s^2 - \mathbf{s}\cdot\mathbf{t}\) and …