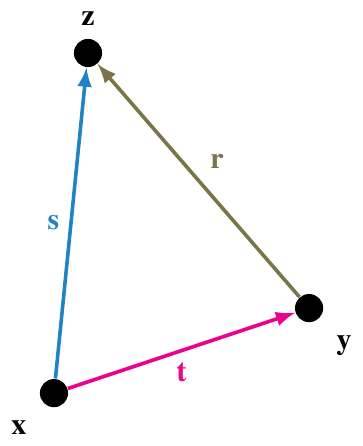
Just a quick mathematical observation for today (actually yesterday): suppose you have three points. Any function of the three points which doesn’t depend on their absolute location or orientation only depends on the magnitudes of the vectors joining the three points.

Suppose the three points are \(\mathbf{x}\), \(\mathbf{y}\), and \(\mathbf{z}\). A function that doesn’t depend on the absolute location of the points will only depend on the displacements between them, \(\mathbf{r} = \mathbf{z} - \mathbf{y}\), \(\mathbf{s} = \mathbf{z} - \mathbf{x}\), and \(\mathbf{t} = \mathbf{y} - \mathbf{x}\). And a function that doesn’t depend on the orientations will only depend on the scalar quantities we can form out of these displacements: \(r^2\), \(\mathbf{r}\cdot\mathbf{s}\), \(s^2\), \(\mathbf{s}\cdot\mathbf{t}\), \(t^2\), and \(\mathbf{t}\cdot\mathbf{r}\). But the dot products are actually not independent, because for example

so,

Then you can write \(\mathbf{r}\cdot\mathbf{s} = s^2 - \mathbf{s}\cdot\mathbf{t}\) and …

I’ve noticed that (many of) my intro-level physics students, who have typically just learned about vectors within the past year, have a hard time working with them in equations. For example, given an equation like \(\sum\vec{F} = m\vec{a}\), I’ll typically think of the force vectors in a geometrical representation, as arrows. Vector addition is done by starting each vector from the endpoint of the previous one in the sum, and scalar multiplication just means scaling the length of the arrow. But almost invariably, whenever I try to walk a student through this representation, they don’t get it. It seems like they’re really not prepared to accept the idea of doing math on things that they can’t plug into their calculators.

What I’ve found to work is this: I tell the students that whenever they see a vector equation, write one copy of it for each dimension. Newton’s second law, for example, becomes a set of three: \(\sum F_x = m a_x\), \(\sum F_y = m a_y\), and \(\sum F_z = m a_z\). That way, all they have to deal with are simple numerical equations. Sure, they miss out on understanding the true nature …